解析:处于光滑水平面的小车,当木块在其上表面滑动时,它们之间有相对运动而存在滑动摩擦力,致使两物均产生加速度,使木块做减速运动,小车做加速运动,这对滑动摩擦力的作用效果是使两物体相对运动的速度减小,当它们相对静止时,由于滑动摩擦力消失而使它们的加速度也随之消失,它们以后将做匀速直线运动.本题的突破点是要能分析到它们之间由相对运动到相对静止这一过程的运动时间和它们各自的位移(对地).
解法一:(1)木块和小车在水平方向上均受到它们之间的滑动摩擦力的作用,摩擦力的大小为f=μmg,由牛顿第二定律
对木块有μmg=mam,am=μg=2m/s2,方向向左;对小车有μmg=MaM,aM=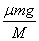 =0.5m/s2,方向向右. =0.5m/s2,方向向右.
由于木块的加速度方向与速度方向相反,故木块做减速运动,小车的初速度为零,故小车在滑动摩擦力的作用下向右做加速运动,当两者速度相等时,它们之间无相对运动,滑动摩擦力立即消失,以后它们一起做匀速运动.
木块的速度vm=v0-amt=v0-μgt
小车的速度vM=aMt=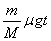
vm=vM时,v0-μgt=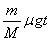 得 得

(2)木块与小车相对静止时,它们的速度为v=v0-μgt=1m/s,在木块相对小车滑动的这段时间内,木块的位移为sm,小车的位移为sM,由位移与平均速度和时间的关系有sm=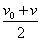 ·t=6m,SM= ·t=6m,SM=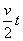 =1m. =1m.
解法二:(1)由解答一可知木块和小车的加速度分别为am=2m/s2方向向左和aM=0.5m/s2方向向右.以小车为参考系,木块初速度v0′=v0=5m/s,加速度a=am+aM=(2+0.5)m/s2=2.5m/s2,当木块做匀减速运动,速度为零时,有
vt=v0′-at=0,t=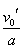 =2s =2s
(2)木块在小车上相对运动的过程中,木块对地的位移为sm,小车对地的位移为sM,由匀变速运动的位移公式可得
sm=v0t- =6m =6m
sM=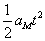 =1m =1m
|