| 系统牛顿第二定律(质点系牛顿第二定律) |
主编:黄冈中学物理集体备课组
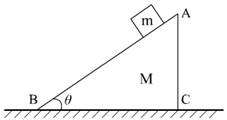
1、质量M=10kg的木楔ABC静止于粗糙水平地面上,如图,动摩擦因数μ=0.02,在木楔的倾角α=30°的斜面上,有一质量m=1.0kg的物块,由静止开始沿斜面下滑,当滑行至s=1.4m时,速度v=1.4m/s,在这过程木楔没有动.求地面对木楔的摩擦力的大小、方向和地面对木楔的支持力.(g=10m/s2)
解法一:(隔离法)
先隔离物块m,根据运动学公式得:
v2=2as
=0.7m/s2<gsinθ=5m/s2
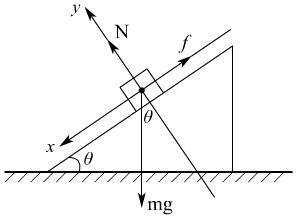
可见物块m受到沿斜面向上的滑动摩擦力,对物体m为对象
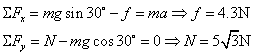
对斜面M:假设地面对M静摩擦力向右:
f地+N′sin30°-f′cos30°=0
而N′=N=
,f′=f=4.3N
f地=-Nsin30°+fcos30°=-0.61N
说明地面对斜面M的静摩擦力f地=0.61N,负号表示方向水平向左.
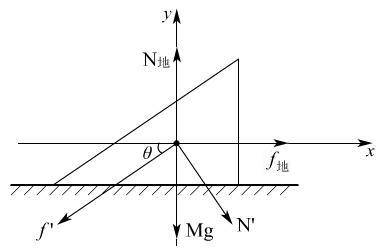
可求出地面对斜面M的支持力N地
N地-f′sin30°-N′cos30°-Mg=0
N地= fsin30°+ Ncos30°+Mg=109.65N<(M+m)g=110N
因m有沿斜面向下的加速度分量,故整体可看作失重状态
方法二:当连接体各物体加速度不同时,常规方法可采用隔离法,也可采用对系统到牛顿第二定律方程.
=m1a1x+m2a2x+…+mnanx
=m1a1y+m2a2y+…+mnany
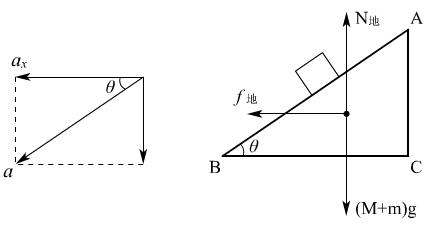
解法二:系统牛顿第二定律:
把物块m和斜面M当作一个系统,则:
x:f地=M×0 +macos30°=0.61N水平向左
y:(M+m)g-N地=M×0+masin30°
N地=(M+m)g-ma sin30°=109.56N
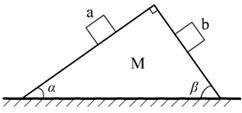
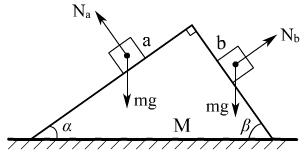
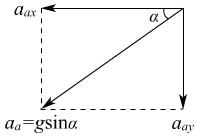
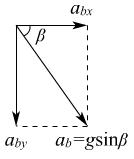
例2:如图所示,一质量为M的楔形木块放在水平桌面上,它的顶角为90°,两底角为α和β;a、b为两个位于斜面上质量均为m的小木块.已知所有接触面都是光滑的,现发现a、b沿斜面下滑,而楔形木块静止不动,求楔形木块对水平桌面的压力和静摩擦力
解法一:隔离法
Na=mgcosα
Nb=mgcosβ
N地=mg+mgcosβsinα+mgcosαsinβ
=Mg+mg(sin2α+cos2α)
=Mg+mg
f地=Nb′cosα-Na′cosβ=mgcosβcosα-mgcosαcosβ=0N
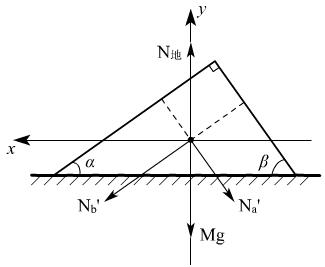
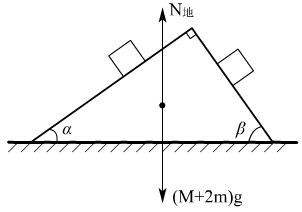
解法二:系统牛顿第二定律列方程:
(M+2m)g-N地=M×0+mgsin2α+mgsin2β
N地=(M+m)g
向右为正方向:f地= M×0+mgsinαcosα-mgsinβcosβ=0
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -