例1、半径为R的球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,滑轮到球面B的距离为h,轻绳的一端系一小球,靠放在半球上的A点,另一端绕过定滑轮后用力拉住,使小球静止,如图1-1所示,现缓慢地拉绳,在使小球由A到B的过程中,半球对小球的支持力N和绳对小球的拉力T的大小变化的情况是( )
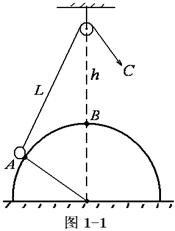
A.N变大,T变小 B.N变小,T变大
B.N变小,T先变小后变大 D.N不变,T变小
解析:
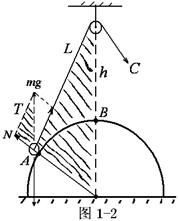
如图1-2所示,对小球:受力平衡,由于缓慢地拉绳,所以小球运动缓慢视为始终处于平衡状态,其中重力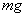 不变,支持力
不变,支持力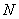 ,绳子的拉力
,绳子的拉力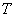 一直在改变,但是总形成封闭的动态三角形(图1-2中小阴影三角形)。由于在这个三角形中有四个变量:支持力
一直在改变,但是总形成封闭的动态三角形(图1-2中小阴影三角形)。由于在这个三角形中有四个变量:支持力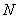 的大小和方向、绳子的拉力
的大小和方向、绳子的拉力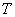 的大小和方向,所以还要利用其它条件。实物(小球、绳、球面的球心)形成的三角形也是一个动态的封闭三角形(图1-2中大阴影三角形),并且始终与三力形成的封闭三角形相似,则有如下比例式:
的大小和方向,所以还要利用其它条件。实物(小球、绳、球面的球心)形成的三角形也是一个动态的封闭三角形(图1-2中大阴影三角形),并且始终与三力形成的封闭三角形相似,则有如下比例式:
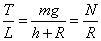
可得: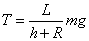 运动过程中
运动过程中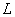 变小,
变小, 变小。
变小。
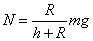 运动中各量均为定值,支持力
运动中各量均为定值,支持力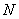 不变。正确答案D。
不变。正确答案D。
例2、如图2-1所示,竖直绝缘墙壁上的Q处由一固定的质点A,在Q的正上方的P点用细线悬挂一质点B,A、B两点因为带电而相互排斥,致使悬线与竖直方向成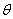 角,由于漏电使A、B两质点的电量逐渐减小,在电荷漏空之前悬线对悬点P的拉力T大小( )
角,由于漏电使A、B两质点的电量逐渐减小,在电荷漏空之前悬线对悬点P的拉力T大小( )
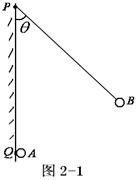
A.T变小 B.T变大
C.T不变 D.T无法确定
解析:
有漏电现象, 减小,则漏电瞬间质点B的静止状态被打破,必定向下运动。对小球漏电前和漏电过程中进行受力分析有如图2-2所示,由于漏电过程缓慢进行,则任意时刻均可视为平衡状态。三力作用构成动态下的封闭三角形,而对应的实物质点A、B及绳墙和P点构成动态封闭三角形,且有如图2-3不同位置时阴影三角形的相似情况,则有如下相似比例:
减小,则漏电瞬间质点B的静止状态被打破,必定向下运动。对小球漏电前和漏电过程中进行受力分析有如图2-2所示,由于漏电过程缓慢进行,则任意时刻均可视为平衡状态。三力作用构成动态下的封闭三角形,而对应的实物质点A、B及绳墙和P点构成动态封闭三角形,且有如图2-3不同位置时阴影三角形的相似情况,则有如下相似比例:
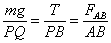
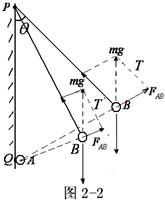
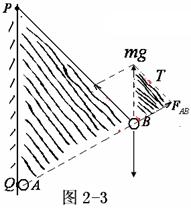
可得: 变化过程PB、PQ、mg均为定值,所以T不变。正确答案C。
变化过程PB、PQ、mg均为定值,所以T不变。正确答案C。
以上两例题均通过相似关系求解,相对平衡关系求解要直观、简洁得多,有些问题也可以直接通过图示关系得出结论。
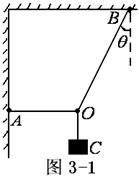
例3、三根细线AO、BO、CO系一重物质量为m如图所示。当A点缓慢上移,且保持O点不动,三根绳上的张力如何变化?如果只有B点缓慢向右移动,且保持O点不动,三根绳上的张力又如何变化?
解析:
本题中有两个研究对象,物体m和悬点O。对物体m处于二力平衡状态有: 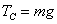 ,如图3-2所示;对悬点O处于三力平衡。由于
,如图3-2所示;对悬点O处于三力平衡。由于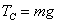 ,所以
,所以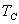 为恒力,
为恒力,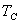 两端点不变。O点、B点不变,又知道
两端点不变。O点、B点不变,又知道 不变。A点“缓慢”上移过程,O点始终处于三力平衡状态,三力始终构成封闭三角形,如图3-2所示A点上移过程中几个状态,可知:
不变。A点“缓慢”上移过程,O点始终处于三力平衡状态,三力始终构成封闭三角形,如图3-2所示A点上移过程中几个状态,可知: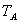 先变小,后变大;
先变小,后变大;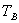 一直变小,
一直变小,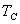 保持不变。
保持不变。
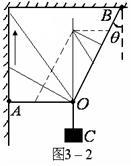
同理如图3-3所示,可分析当A点、O点保持不变, 一直变小,
一直变小,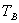 一直变小,
一直变小, 保持不变。
保持不变。
事实上这类问题可以通通归类于矢量三角问题,上述解法对高一同学来说容易理解、接受,高年级同学可以尝试直接用矢量三角方法求解。