1、基本公式法
匀变速直线运动的公式有：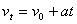
、
、
、
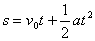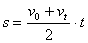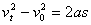，在这些公式中，只涉及五个物理量：初速度v0、末速度vt、加速度a、位移s和时间t。而v0、vt、a、s它们均是矢量，使用时要注意方向性，因是直线运动，一般以v0的方向为正方向，其余与正方向相同者为正，数值取“＋”号，与正方相反者为负，数值取“－”号。当初速度v0=0时，一般以加速度a的方向为正。
2、平均速度法：
平均速度的定义式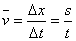
， 对任何性质的运动都适用，而在匀变速直线运动中，整个过程的平均速度等于中间时刻的瞬时速度，也等于初、末速度和的一半，即：
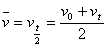，求位移时，可以利用
。
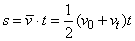3、中间时刻速度法
利用“任意时间t中间时刻的瞬时速度等于这段时间t内平均速度”即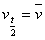
，适用于任何一个匀变速直线运动，有些题目应用它可以避免常规解法中用位移公式列出的含有t2的复杂式子，从而简化解题过程，提高解题速度。
4、比例法
在初速度为零的匀加速直线运动中，有下面几个重要特征的比例关系：
（1）在1T末、2T末、3T末……瞬时速度之比为：
(
)
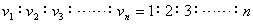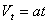（2）在1T内、2T内、3T内……通过的位移之比为：
(
)
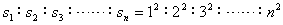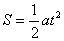（3）在第一个T内、第二个T内、第三个T内……通过的位移之比为：
（
）
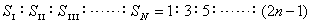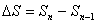（4）在通过第一个S内、第二个S内、第三个S内……所用时间之比为：
（
）
因此，对于初速度为零的匀加速直线运动的某些问题，我们可利用上面几个重要特征的比例关系来求解，有时可达到“出奇兵”的效果。
5、逆向思维法
逆向过程处理（逆向思维法）是把运动过程的“末端”作为“初态”来反向研究问题的方法，如物体做加速运动看成反向的减速运动，物体做减速运动看成反向加速运动处理。该方法一般用在末状态已知的情况，若采用逆向思维方法，将它看作匀加速运动来求解，往往能收到事半功倍的效果。
在处理末速度为零的匀减速直线运动时，可以采用逆推法，将该运动对称的看作是加速度大小相等的初速度为零的匀加速运动，则相应的位移、速度公式以及在连续相等时间的位移之比、连续相等位移内的时间之比等结论，均可使用，采用这种方法尤其在解选择题或填空题时十分简捷。
6、图像法
利用图像解题可以使解题过程简化，思路更清晰，比解析法更巧妙、更灵活。从物理图象可以更直接地观察出物理过程的动态特征，尤其是用图像定性分析，可避开繁杂的计算，快速找出答案。
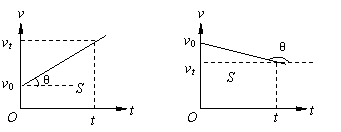
对匀变速直线运动，运用v－t图像分析解答问题比较常见，运用时须理解图像的物理意义：
截距：初速度v0；坐标（t，v0）：t时刻的瞬时速度；
直线的斜率：tanθ＝a（加速度）；坐标轴和图像围成的面积：t时间内的位移，并且要注意各物理量的正负号的物理意义。
7、巧用推论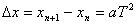
匀变速直线运动中，在连续相等的时间T内的位移之差为一恒量，即
，对一般的匀变速直线运动问题，若出现相等的时间间隔问题，可优先考虑用
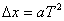求解。
8、巧取参考系，将物体的运动简化
运动都是相对于某一参考系而言的，同一运动相对于不同的参考系，会有不同的结果。比如，一辆匀速运动的汽车，对等速同向运动的汽车与速度比它大的同向运动汽车，分别是静止和向后运动。
研究地面上物体的运动，常以地面为参考系，有时为了研究的方便，也可以巧妙地选用其他物体做参考系（如两车的追击问题、同时开始的自由落体问题等），从而可简化求解过程。
选取参考系的一般原则是：使研究对象的运动尽量变得简单。
例题1、原地起跳时，先屈腿下蹲，然后突然蹬地。从开始蹬地到离地是加速过程（视为匀加速），加速过程中重心上升的距离称为“加速距离”。离地后重心继续上升，在此过程中重心上升的最大距离称为“竖直高度”。现有下列数据：人原地上跳的“加速距离”d1＝0.50m，““竖直高度”h1＝1.0m；跳蚤原地上跳的“加速距离”d2＝0.00080m，“竖直高度” h2＝0.10m。假想人具有与跳蚤相等的起跳加速度，而“加速距离”仍为0.50m，则人上跳的“竖直高度”是多少？
解法一（基本公式法）：
用a 表示跳蚤起跳的加速度，v表示离地时的速度，则对加速过程和离地后上升过程分别有：
v2 ＝2ad2
v2 ＝2gh2
若假想人具有和跳蚤相同的加速度a ，令v表示在这种假想下人离地时的速度，H表示与此相应的竖直高度，则对加速过程和离地后上升过程分别有：
v2＝2ad1
v2＝2gH
由以上各式可得: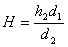
代入数值，得H=62.5m
解法二（图象法）：
题目要求人和跳蚤的加速度相同，故其图像的斜率相同，起跳后都是竖直上抛运动，故第二阶段的斜率也相同，其v－t图像如下图所示。
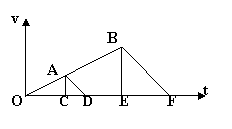
d1为三角形OBE的面积，d2为三角形OAC的面积，h2为三角形ACD的面积，则人上跳的“竖直高度”是三角形BEF的面积。
有几何关系可得：
代入数值，得H=62.5m
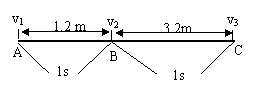
例题2、一物体做匀加速直线运动，已知在相邻的两个1s内通过的位移分别为1.2m和3.2m，求物体的加速度a和相邻的两个1s内的初、末速度v1、v2、v3。
解法一（基本公式法）：
画出示意图如下图所示，根据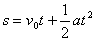
，有
，
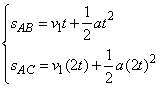即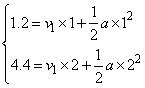
，
解出：
由速度公式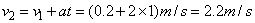
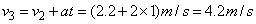
解法二（利用推论）：
由于物体做匀加速直线运动，且tAB=tBC=t=1s，利用相邻的相等时间内的位移差等于恒量at2的推论，即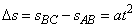
，
所以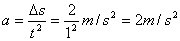 
再根据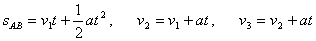
可求出：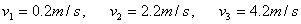
解法三（平均速度法）：
物体在AC段平均速度等于中间时刻B点的瞬时速度，即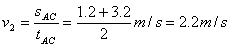
。
同理：可求出AB段、BC段的中间时刻D、E两点的瞬时速度vD、vE，
， 
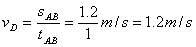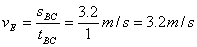
又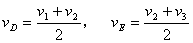 
所以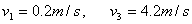 
而物体加速度为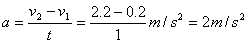 
例题3、一列车有等长的车厢连接而成，车厢之间的间隙忽略不计，一人站在站台上与第一节车厢的最前端相齐，当列车由静止开始作匀加速直线运动时开始计时，测得第一节车厢通过他的时间为2s，则从第5节至第16节车厢通过他的时间为多少？
分析：
此题若以车为研究对象，由于车不能简化为质点，因此我们取车为参考系，把车的运动转化为人做匀加速直线运动来考虑，则这题就简单了很多。 根据通过连续相等的位移所用时间之比为：
，
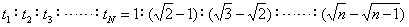则可得：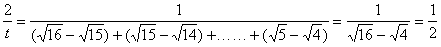
，
所以所求时间为：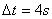
例题4、一物块以一定的初速度从光滑斜面底端a点上滑，最高可滑至b点，c是ab的中点，如下图所示，已知物块从a至c需要的时间为t0，问它从c经b再回到c，需要的时间是多少？
分析：
本题解法有多种，但若采用逆推法，则会将问题简化很多。采用逆推法：将滑块的运动视为由b点开始下滑的匀加速直线运动，已知通过第二段相等位移ca的时间为t0，因此只要求出通过第一段相等位移bc所需的时间tbc，那么2tbc就是所求时间。
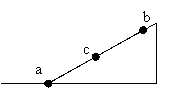
解：
根据初速度为零的匀加速直线运动在通过连续相等位移所用的时间之比的结论：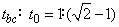
可得：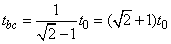
故物块从c经b再回到c的时间为：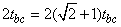
运动学问题的分析的方法是多种多样，但总有一些解法比较简单，希望在掌握基本分析方法的基础上多考虑一些不同解题方法。以上仅仅列举了部分实例，而且也并非每一题都穷举了求解方法，其意在对问题的分析起抛砖引玉的作用，启迪学生不要麻木做题而沉埋于题海中，要通过精解习题，来激活思维，寻找共性，来不断地提高分析能力、整合能力、探究能力和解决问题的能力。
