| 追及和相遇问题 |
主编:黄冈中学物理集体备课组
引入:两个物体在同一直线上运动,往往涉及追及、相遇和避免碰撞问题.本节课我们就应用前面所学的匀变速直线运动的规律来解决追及和相遇问题.
一、追及问题:追和被追的两物体同向运动,当速度相等是能否追上或两者距离有最大值、最小值的临界条件.
常见情形有三种:
①同时同地出发:初速为零的匀加速直线运动物体甲追匀速运动的物体乙:一定能追上,当v甲=v乙时,两者之间有△smax.
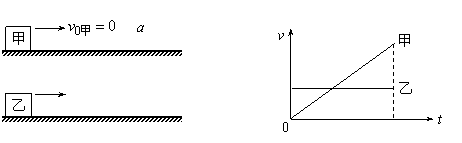
②同时不同地:速度大的匀速运动物体甲追赶同方向匀加速运动的物体乙.(v甲>v乙)
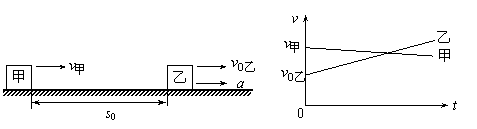
A.当v乙=v甲时,s甲=s0+s乙,甲恰好追上乙
B.当v乙=v甲时,s甲<s0+s乙,甲永远追不上乙,此时两者有最小间距△smin
C.当v乙<v甲时,s甲>s0+s乙,甲追上了乙,由于乙作匀加速运动,以后v乙>v甲,则乙还有一次追上甲的机会,其间两者速度相等时两者距离有一个较大值
③同地不同时:
二、相遇问题:相遇问题分为追及相遇和相向相遇问题,上面三种常见问题属于追及相遇问题.至于相向相遇问题,我们通过例题来进行说明,本节课重点解决追及相遇问题.
对于追及相遇问题,我们解题过程中要弄清物体的运动过程,挖掘题中隐含的临界条件,在解题方法上常常用到解析法、数学法、图象法、相对运动等方法.
例、火车以速度v1匀速行驶,司机发现前方同轨道上相距s处有另一火车沿同方向以速度v2(对地,且v1>v2)做匀速运动,司机立即以加速度a紧急刹车,要使两车不相撞,a应满足什么条件?
分析:
后面火车刹车后虽然做匀减速运动,但在其速度减小至与v2相等之前,两车的距离将逐渐减小;当后车速度减为前车速度后,两车距离将逐渐增大.可见,当两车速度相等,两车距离最近.若后车减速的加速度过小,则会出现后车速度减为与前车速度相等之前,已追上前车,发生撞车事故;若后车加速度过大,则会出现后车速度减为与前车速度相等时未追上前车,不会发生撞车事故;若后车加速度大小等于某值时,恰能使两车在速度相等时后车追上前车,这正是两车不相撞的临界条件,此加速度即为两车不相撞的最小加速度.
解法一(解析法):
设经时间t,当v1-at=v2时,后车恰好追上前车而不相撞,则
v1t-
v2t+s
时两车不会相撞
解法二(数学法):
要使两车不相撞,其位移关系满足:
v1t-
v2t+s
即
+(v2-v1)t+s
0对任意时间t上述不等式成立
△=(v1-v2)2-2as
0
解法三(图象法):
两火车的v-t图象如图所示,使两车不相撞,则当后车速度减小至等于v2时,后车比前车多走位移小于开始刹车时两车间距s,就不会相撞.
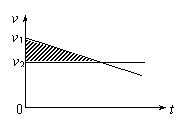
解法四(相对运动法):
以前车为参考系,刹车后,后车相对前车做初速为v0=v1-v2,加速度大小为a的匀减速直线运动.当后车相对前车的速度减为零时,若相对位移
≥s,则不会相撞.由
.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -