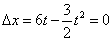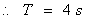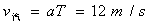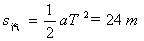例、一辆汽车在十字路口等候绿灯，当绿灯亮时汽车以3m/s2的加速度开始加速行驶，恰在这时一辆自行车以6m/s的速度匀速驶来，从后边超过汽车。试求：汽车从路口开动后，在追上自行车之前经过多长时间两车相距最远？此时距离是多少？
解1：（公式法）
当汽车的速度与自行车的速度相等时，两车之间的距离最大。设经时间t两车之间的距离最大。则
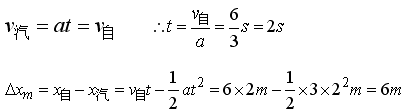
解2：（图像法）
在同一个v－t图中画出自行车和汽车的速度时间图像，根据图像面积的物理意义，两车位移之差等于图中梯形的面积与矩形面积的差，当t=t0时矩形与三角形的面积之差最大。
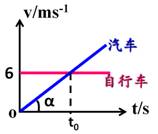
v－t图像的斜率表示物体的加速度
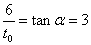
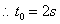
当t=2s时两车的距离最大为图中阴影三角形的面积
动态分析随着时间的推移，矩形面积（自行车的位移）与三角形面积（汽车的位移）的差的变化规律
解3：（相对运动法）
选自行车为参照物，以汽车相对地面的运动方向为正方向，汽车相对自行车沿反方向做匀减速运动v0=－6m/s，a=3m/s2，两车相距最远时vt=0
对汽车由公式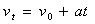 
（由于不涉及位移，所以选用速度公式。）
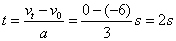
对汽车由公式：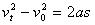
（由于不涉及“时间”，所以选用速度位移公式。）
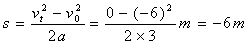
表示汽车相对于自行车是向后运动的，其相对于自行车的位移为向后6m.
解4：（二次函数极值法）
设经过时间t汽车和自行车之间的距离Δx，则
，
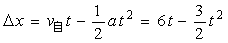
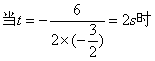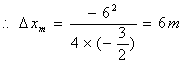
思考：汽车经过多少时间能追上摩托车?此时汽车的速度是多大?汽车运动的位移又是多大？
