解析:由于两车同时同向运动,故有v甲=v0+a2t,v乙=a1t
①当a1<a2时,a1t<a2t,可得两车在运动过程中始终有v甲>v乙.由于原来甲在后,乙在前,所以甲、乙两车的距离在不断缩短,经过一段时间后甲车必然超过乙车,且甲车超过乙车后相距越来越大,因此甲、乙两车只能相遇一次.②当a1=a2时,a1t=a2t,可得v甲>v乙,因此甲、乙两车也只能相遇一次.③当a1>a2时,a1t>a2t,v甲和v乙的大小关系会随着运动时间的增加而发生变化,刚开始,a1t和a2t相差不大且甲有初速v0,所以v甲>v乙;随着时间的推移,a1t和a2t相差越来越大;当a1t-a2t=v0时,v甲=v乙,接下来a1t-a2t>v0,则有v甲<v乙.若在v甲=v乙之前,甲车还没有超过乙车,随后由于v甲<v乙,甲车就没有机会超过乙车,即两车不相遇;若在v甲=v乙时,两车刚好相遇,随后v甲<v乙,甲车又要落后乙车,这样两车只能相遇一次;若在v甲=v乙前,甲车已超过乙车,即已相遇过一次,随后由于v甲<v乙,甲、乙距离又缩短,直到乙车反超甲车时,再相遇一次,则两车能相遇两次.
解法一:由于x甲=v0t+
x乙=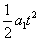
相遇时有x甲-x乙=s
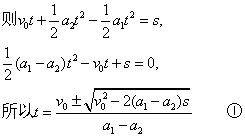
①当a1<a2时,①式t只有一个正解,则相遇一次.
②当a1=a2时,x甲-x乙= =v0t=s. =v0t=s.
所以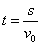 ,t只有一个解,则相遇一次. ,t只有一个解,则相遇一次.
③当a1>a2时,若v02<2(a1-a2)s,①式无解,即不相遇.
若v02=2(a1-a2)s,①式t只有一个解,即相遇一次.
若v02>2(a1-a2)s,①式t有两个正解,即相遇两次.
解法二:(利用v-t图象求解)
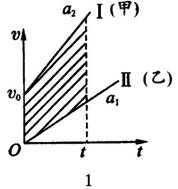
①当a1<a2时,甲、乙两车的运动图线分别为如图1中的I和Ⅱ,其中划斜线部分的面积表示t时间内甲车比乙车多发生的位移,若此面积S=s,则t时刻甲车追上乙车而相遇,以后在相等时间内甲车发生的位移都比乙车多,所以只能相遇一次.
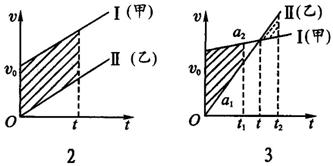
②当a1=a2时,甲、乙两车的运动图线分别为如图2中的I和II,讨论方法同①,所以两车也只能相遇一次.
③当a1>a2时,甲、乙两车的运动图线分别为如上图3中的I和Ⅱ,其中划实斜线部分的面积表示甲车比乙多发生的位移.若划实斜线的部分面积小于s,则不能相遇;若划实斜线部分面积等于s,说明甲车刚追上乙车又被反超,则相遇一次;若划实斜线部分的面积大于s,如图中0~t1内划实斜线部分的面积为s,说明t1时刻甲车追上乙车,以后在t1~t时间内,甲车超前乙车的位移为t1~t时间内划实斜线部分的面积,随后在t~t2时间内,乙车比甲车多发生划虚线部分的面积,如果两者相等,则t2时刻乙车反超甲车,故两车先后相遇两次. |