|
11、解:(1)证明:设A、B的横坐标分别为x1、x2,由题设知x1>1,x2>1,点A(x1,log8x1),B(x2,log8x2).
因为A、B在过点O的直线上,所以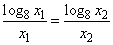 ,又点C、D的坐标分别为(x1,log2x1)、(x2,log2x2). ,又点C、D的坐标分别为(x1,log2x1)、(x2,log2x2).
由于log2x1=3log8x1,log2x2=3log8x2,则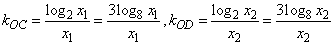 . .
由此得kOC=kOD,即O、C、D在同一直线上.
(2)解:由BC平行于x轴,有log2x1=log8x2,又log2x1=3log8x1.
∴x2=x13,将其代入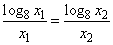 ,得x13log8x1=3x1log8x1, ,得x13log8x1=3x1log8x1,
由于x1>1知log8x1≠0,故x13=3x1,x1= ,于是A( ,于是A(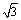 ,log8 ,log8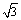 ). ). |