直线系方程及其应用
一般地说具有某种共同属性的一类直线的集合，称为直线系．
(1)已知直线l:Ax＋By＋C=0，则和l平行的直线系方程为Ax＋By＋m=0(m为参数，m≠C)．和l垂直的直线系方程为Bx－Ay＋n=0(n为参数)．
(2)经过两直线交点的直线系方程为A1x＋B1y＋C1＋λ(A2x＋B2y＋C2)=0．
例、求经过两直线l1:x－2y＋4=0和l2：x＋y－2=0的交点P，并且与直线l3:3x－4y＋5=0垂直的直线l的方程．
分析：本题可先通过解方程组求出点P的坐标，再利用l⊥l3，求得直线l的斜率，最后利用点斜式求出l的方程，也可用直线系方程求解．
解法1：解方程组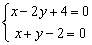
，得交点P(0,2)．
∵l⊥l3，且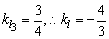
．
由点斜式得直线l的方程为4x＋3y－6=0．
解法2：设所求直线l的方程为(x－2y＋4)＋λ(x＋y－2)=0，
整理得(1＋λ)x＋(λ－2)y＋4－2λ=0．
∴(λ＋1)×3＋(λ－2)×(－4)=0，得λ=11．
故所求直线l的方程为4x＋3y－6=0．
