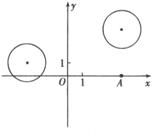
例、（江苏卷）在平面直角坐标系xOy中，已知圆C1：（x＋3）2＋(y－1)2=4和圆C2：（x－4）2＋(y－5)2=4.
（1）若直线l过点A（4，0），且被圆C1截得弦长为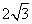
，求直线l的方程；
（2）设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l1和l2，它们分别与圆C1和C2相交，且直线l1被圆C1截得弦长与直线l2被圆C2截得的弦长相等．试求所有满足条件的点P的坐标．
答案：
本小题主要考查直线与圆的方程、点到直线的距离公式等基础知识，考查数学运算求解能力、综合分析问题的能力．
解析：
（1）由于直线x=4与圆C1不相交，所以直线l的斜率存在．
设直线l的方程为y=k(x－4)，圆C1的圆心到直线l的距离为d，
因为圆C1被直线l截得的弦长为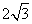
，所以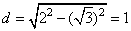
.
由点到直线的距离公式得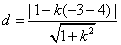
，
从而k(24k＋7)=0，即k=0或k=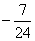
，
所以直线l的方程为y=0或7x＋24y－28=0.
（2）设点P（a，b）满足条件，不妨设直线l1的方程为y－b=k(x－a)，k≠0，
则直线l2的方程为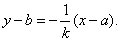
因为圆C1和C2的半径相等，及圆C1被直线l1截得的弦长与圆C2被直线l2截得的弦长相等，所以圆C1的圆心到直线l1的距离和圆C2的圆心到直线l2的距离相等，
即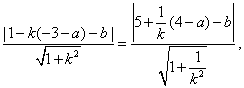
整理得|1＋3k＋ak－b|=|5k＋4－a－bk|，从而1＋3k＋ak－b=5k＋4－a－bk或1＋3k＋ak－b=－5k－4＋a＋bk，即(a＋b－2)k=b－a＋3或（a－b＋8）k=a＋b－5，因为k的取值有无穷多个，所以
