圆与圆的位置关系同步测试
一、选择题
1、两圆和的位置关系是（ ） A．相离 B．相交 C．内切 D．外切 2、圆：和圆：交于两点，则AB的垂直平分线的方程是（ ） A． B． C． D． 3、已知圆x2＋y2＝9与圆x2＋y2－4x＋4y－1＝0关于直线l对称，则直线l的方程为（ ） A．4x－4y＋1＝0 B．x－y＝0 C．x＋y＝0 D．x－y－2＝0 4、设O为坐标原点，C为圆（x－2）2＋y2＝3的圆心，且圆上有一点M（x，y）满足＝0，则＝（ ） A． B．或－ C． D．或－ 5、设集合A={(x，y)|x2＋y2≤4}，B={(x，y)|(x－1)2＋(y－1)2≤r2(r＞0)}，当A∩B=B时，r的取值范围是（ ） A．（0，－1） B．（0，1] C．（0，2－] D．（0，]
1、两圆和的位置关系是（ ）
A．相离 B．相交 C．内切 D．外切
A．相离 B．相交
C．内切 D．外切
2、圆：和圆：交于两点，则AB的垂直平分线的方程是（ ）
A． B． C． D．
A． B．
C． D．
3、已知圆x2＋y2＝9与圆x2＋y2－4x＋4y－1＝0关于直线l对称，则直线l的方程为（ ）
A．4x－4y＋1＝0 B．x－y＝0 C．x＋y＝0 D．x－y－2＝0
A．4x－4y＋1＝0 B．x－y＝0
C．x＋y＝0 D．x－y－2＝0
4、设O为坐标原点，C为圆（x－2）2＋y2＝3的圆心，且圆上有一点M（x，y）满足＝0，则＝（ ）
A． B．或－ C． D．或－
A． B．或－
C． D．或－
5、设集合A={(x，y)|x2＋y2≤4}，B={(x，y)|(x－1)2＋(y－1)2≤r2(r＞0)}，当A∩B=B时，r的取值范围是（ ）
A．（0，－1） B．（0，1] C．（0，2－] D．（0，]
A．（0，－1） B．（0，1]
C．（0，2－] D．（0，]
提示：
二、填空题
6、过两圆C1：（x－4）2＋（y－5）2＝10，C2：（x＋2）2＋（y－7）2＝12，交点所在的直线方程为_________________． 7、两圆－6x＋6y－48＝0与＋4x－8y－44＝0公切线的条数是__________．
6、过两圆C1：（x－4）2＋（y－5）2＝10，C2：（x＋2）2＋（y－7）2＝12，交点所在的直线方程为_________________．
7、两圆－6x＋6y－48＝0与＋4x－8y－44＝0公切线的条数是__________．
三、解答题
8、已知圆，圆，问为何值时，（1）圆与圆相外切；（2）圆与圆相内含．
8、解：，．
(1)两圆外切，则有，解得或；
(2)两圆内含，则有，解得．
9、求两圆和的公切线方程．
9、解：圆，.
易知两圆相离．
先求外公切线的方程．
设它们的交点为，
则点分的比，
由定比分点公式得，
设外公切线的方程为，由圆心到其距离为1，得
或．
故两圆的外公切线方程为或．
同理可求得内公切线方程为或．
10、如下图所示，已知圆C1：x2＋y2－2mx－2ny＋m2－1＝0和圆C2：x2＋y2＋2x＋2y－2＝0交于A、B两点且这两点平分圆C2的圆周． 求圆C1的圆心C1的轨迹方程，并求出当圆C1的半径最小时圆C1的方程．
10、如下图所示，已知圆C1：x2＋y2－2mx－2ny＋m2－1＝0和圆C2：x2＋y2＋2x＋2y－2＝0交于A、B两点且这两点平分圆C2的圆周．
求圆C1的圆心C1的轨迹方程，并求出当圆C1的半径最小时圆C1的方程．
10、解：圆C1：(x－m)2＋(y－n)2＝n2＋1，圆C2：(x＋1)2＋(y＋1)2＝4，而C1C2⊥AB且AB为圆C2直径．
∴|AC2|＝2，又|AC1|2＝1＋n2，|AC2|2＝4，|C1C2|2＝(m＋1)2＋(n＋1)2．
在Rt△AC2C1中，由勾股定理，得4＋(m＋1)2＋(n＋1)2＝1＋n2，∴(m＋1)2＝－2(n＋2)即为点C1的轨迹方程．
又－2(n＋2)≥0，n≤－2，当n＝－2时，m＝－1，
圆C1半径最小值为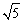，此时圆C1的方程为(x＋1)2＋(y＋2)2＝5．
11、如图，圆O1与圆O2的半径都是1，O1O2=4，过动点P分别作圆O1、圆O2的切线PM、PN（M、N分别为切点），使得，试建立适当的坐标系，并求动点P的轨迹方程．
11、解：以O1O2的中点O为原点，O1O2所在的直线为x轴，建立平面直角坐标系，则O1(－2，0)，O2(2，0)，
由已知，得．
因为两圆的半径均为1，所以．
设，则，
即，
所以所求轨迹方程为．
-END-
和
的位置关系是
和圆：
交于
两点，则AB的垂直平分线的方程是
B．
D．
＝0，则
＝
B．
或－
D．
或－
－1） B．（0，1]
] D．（0，
]
－6x＋6y－48＝0与
＋4x－8y－44＝0公切线的条数是__________．
，圆
，问
为何值时，（1）圆
与圆
相外切；（2）圆
与圆
相内含．
，
．
，解得
或
；
，解得
．
和
的公切线方程．
，
.
，
分
的比
，
，
，由圆心
到其距离为1，得
或
．
或
．
或
．
，此时圆C
，试建立适当的坐标系，并求动点P的轨迹方程．
，得
．
．
，则
，
，
．