| 空间直角坐标系 |
主编:黄冈中学数学集体备课组
一、知识概述
空间中点
、
间的距离公式:
.
二、例题讲解
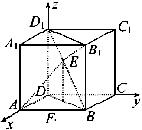
例1、已知正四棱锥P—ABCD的底面边长为4,侧棱长为10,试建立适当的空间直角坐标系,写出各顶点的坐标.
解:
法一:如图(见视频),以D为坐标原点,以DA所在直线为x轴,DC所在直线为y轴,建立空间直角坐标系.
则D(0,0,0),A(4,0,0),C(0,4,0),B(4,4,0),P(2,2,
).
法二:A(
,0,0),B(0,
,0),C(-
,0,0),D(0,-
,0),P(0,0,
).
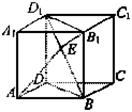
例2、如图,已知正方体ABCD—A1B1C1D1的棱长为a,过点B1作B1E⊥BD1于点E,求A、E两点之间的距离.
解析:
以D为坐标原点,以DA、DC、DD1所在直线为x、y、z轴,建立空间直角坐标系.
由题意得D(0,0,0),A(a,0,0),C(0,a,0),B(a,a,0),B1(a,a,a).
过点E作EF⊥BD于点F,则EF//DD1,又DD1⊥平面ABCD,∴EF⊥平面ABCD.
连接B1D1,则B1D1=
.
在
.
又EF//DD1,
.
.
∴
所以A、E两点之间的距离是
.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -