例1、（辽宁卷）在正方体ABCD－A1B1C1D1中，E、F分别为棱AA1、CC1的中点，则在空间中与三条直线A1D1、EF、CD都相交的直线（ ）
A．不存在 B．有且只有两条
C．有且只有三条 D．有无数条
答案：D
解析：
分别在异面直线A1D1、CD上各任取一点M、N，则线段MN的中点的轨迹构成一个平面α，显然直线EF在平面α内．在EF上任取一点P，点P和直线A1D1确定的平面与直线CD交于点Q，显然直线QP与直线A1D1必有交点R，即这样的直线有无穷多条．故选D．
例2、（全国Ⅱ卷）已知正四棱柱ABCD－A1B1C1D1中，AA1=2AB，E为AA1中点，则异面直线BE与CD1所成角的余弦值为（ ）
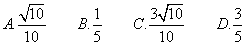
答案：C
解析：
连结A1B，则有A1B//CD1．
∴∠A1BE就是异面直线BE与CD1所成的角，设AB=1，则A1E=AE=1，
例3、(全国卷)已知m，n为异面直线，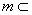
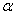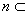平面
，
平面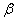
，
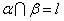，则l（ ）
A．与m，n都相交
B．与m，n中至少一条相交
C．与m，n都不相交
D．至多与m，n中一条相交
解析：
m，n两条直线不可能都不与交线相交，否则m，n平行，故C错．但也可能有一条与交线平行，另一条与交线相交，也可能两条都与交线相交．故选B．
点拨：
本题也可用排除法来解答．
例4、(高考)已知a、b为不垂直的异面直线，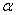
是一个平面，则a、b在
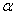上的射影有可能是①两条平行线；②两条互相垂直的直线；③同一条直线；④一条直线及其外一点．在上面的结论中，正确结论的编号是_________．（写出所有正确结论的编号）．
解析：
拿两支笔或小棍作为不垂直的异面直线，向水平桌面上投影，易验证①②④正确．又设a、b在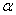
上的射影为同一条直线，则a、b必共面，这与a、b是异面直线矛盾．故③不正确．
故正确结论的是①②④．
