| 空间直线与直线间的位置关系 |
主编:黄冈中学数学集体备课组
一、知识概述
1、空间中的直线的位置关系:平行、相交、异面.
2、异面直线:不同在任何一个平面内的两条直线称为异面直线.
3、异面直线的画法:
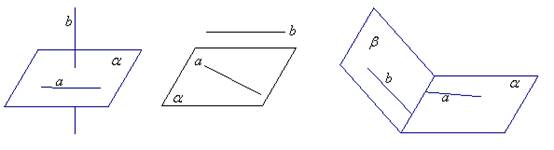
4、公理4:
.
5、定理:空间中两个角的两边分别对应平行,那么这两个角相等或互补.
6、两条异面直线所成的角θ,
.
二、例题讲解
例1、已知空间四边形ABCD中,E、F分别是AB和BC的中点,G、H分别在CD和AD上,且有
.求证:直线EH、FG、BD相交于一点.
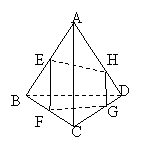
证明:
∵E、F分别是AB和BC的中点,∴EF//AC且EF=
AC.
又∵
,∴GH//AC且GH=
AC(n>2).
∴GH//EF,又GH<EF.
∴EH与FG相交,设交点为P.
∵EH
平面ABD,且P∈EH,∴P∈平面ABD.
同理可证:P∈平面BCD.
又平面BCD∩平面ABD=BD.
∴P∈BD.
∴直线EH、FG、BD相交于一点.
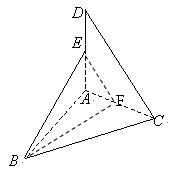
例2、如图,等腰Rt△ABC中,
,若DA=1,且E为DA的中点,求异面直线BE与CD所成角的余弦值.
解:
取AC的中点F,连接EF,BF.
∵E为DA的中点,∴EF//DC.
∴∠BEF或其补角即为异面直线BE与CD所成的角.
∵△ABC为等腰直角三角形,且BC=
.
∴AB=AC=1,在Rt△EAB中,
.
.
.
∴异面直线BE与CD所成角的余弦值为
.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -