A. AC⊥BD
B. AC∥截面PQMN
C. AC=BD
D. 异面直线PM与BD所成的角为45°
答案:C
解析:
∵MN//PQ,∴MN//面ABC,∴MN//AC.
同理BD//QM,∵MN⊥QM,∴AC⊥BD,∴A是对的;
∵AC//MN,∴AC//面PQMN,故B对;
∵BD//QM,∴PM与BD所成角即为∠PMQ,∴PM与BD成45°角,故D对.
故选C.
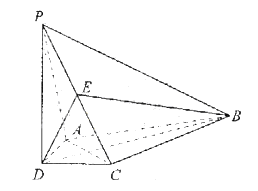
例2、(天津卷)如图,在四棱锥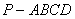 中,
中, ,
,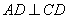 ,且DB平分
,且DB平分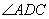 ,E为PC的中点,
,E为PC的中点,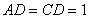 ,
,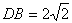 .
.
(1)证明 ;
;
(2)证明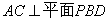 ;
;
(3)求直线BC与平面PBD所成的角的正切值.
(1)证明:
设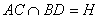 ,连结EH,在
,连结EH,在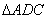 中,因为AD=CD,且DB平分
中,因为AD=CD,且DB平分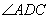 ,所以H为AC的中点,又由题设,E为PC的中点,故
,所以H为AC的中点,又由题设,E为PC的中点,故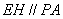 ,
,
又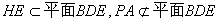 ,所以
,所以 .
.
(2)证明:
因为 ,
, ,所以
,所以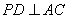 .
.
由(1)知,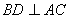 ,又
,又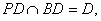 故
故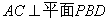 .
.
(3)解:
由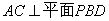 可知,BH为BC在平面PBD内的射影,所以
可知,BH为BC在平面PBD内的射影,所以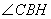 为直线与平面PBD所成的角.
为直线与平面PBD所成的角.
由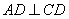 ,
, .
.
在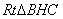 中,
中,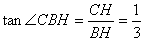 ,
,
所以直线BC与平面PBD所成的角的正切值为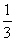 .
.