| 直线与平面的位置关系 |
主编:黄冈中学数学集体备课组
1、空间直线与平面
直线与平面的位置关系有且只有三种:
(1)直线在平面内:有无数个公共点;
(2)直线与平面相交:有且只有一个公共点;
(3)直线与平面平行:没有公共点.
2、直线与平面平行的判定
直线与平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
注意:这个定理是证明直线与平面平行最常用的一个定理,也就是说欲证明一条直线与一个平面平行,一是说明这条直线不在这个平面内,二是要证明已知平面内有一条直线与已知直线平行.
3、直线与平面平行的性质
(1) 直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.
注意:如果一条直线和一个平面平行,那么这条直线和平面内的无数条直线平行,但不能误解为“如果一条直线与一个平面平行,那么这条直线就和平面内的任意一条直线平行”.实际上,如果一条直线和一个平面平行,这条直线和平面内的直线平行或异面,有两种位置关系.
4、直线与平面垂直的判定
(1)直线与平面垂直的定义
如果一条直线和一个平面内的任意一条直线都垂直,我们就说这条直线和这个平面垂直,其中直线叫作平面的垂线,平面叫作直线的垂面.
注意:①定义中的“任意一条直线”和“所有直线”是同义语,不能改成“无穷多条直线”.
②如果
或
,那么直线l不可能与平面α内的任意一条直线都垂直.由此可知,当
时,直线l和α一定相交,它们唯一的交点叫做垂足.
(2)直线和平面垂直的判定定理
如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.
(3)关于垂直的存在唯一性
命题1:过一点有且只有一条直线和已知平面垂直.
命题2:过一点有且只有一个平面和已知直线垂直.
(4)点到平面的距离
从平面外一点引平面的垂线,这个点和垂足间的距离,叫做这个点到这个平面的距离.
5、直线与平面垂直的性质
如果两条直线同垂直于一个平面,那么这两条直线平行.
作用:可作线线平行的判定定理.
6、直线与平面所成的角
(1)直线与平面斜交时,直线与平面所成的角是指这条直线和它在平面上的射影所成的锐角.
(2)直线与平面垂直时,直线与平面所成的角为90°.
(3)直线与平面平行或在平面内时,直线与平面所成的角为0°.
显然,直线与平面所成的角的范围为[0°,90°].
例1.下列说法正确的是( )
A.若直线a平行于平面α内的无数条直线,则
B.若直线a在平面α外,则
C.若直线a//b,直线
,则
D.若直线a//b,直线
,则直线a平行于平面α内的无数条直线
答案:D
例2.如图,E、H分别是空间四边形ABCD的边AB、AD的中点,平面α过EH分别交BC、CD于F、G.求证:EH//FG.
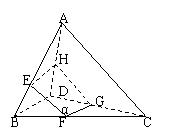
证明:
∵E、H分别是AB、AD的中点,∴EH//BD.
又BD
面BCD,EH
面BCD,
∴EH//面BCD.
又EH
,
面BCD=FG,
∴EH//FG.
例3.如图所示,在正方体ABCD-A1B1C1D1中,E是BB1的中点,O是底面正方形ABCD的中心,求证:OE⊥平面ACD1.
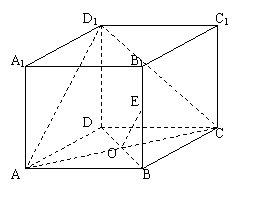
证明:
如图,连接AE、CE、D1O、D1E.
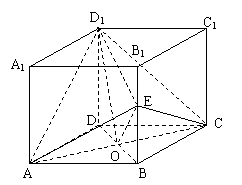
∵AB=BC,B1B⊥面ABCD.∴△ABE≌△CBE,∴AE=CE.
又O为AC的中点,∴OE⊥AC.
设正方体棱长为a.
,
,
.
,
.
面ACD1,
∴OE⊥面ACD1.
例4.P是△ABC外的一点,PA,PB,PC两两垂直,PA=1,PB=2,PC=3,则△ABC的面积为( )
A.
B.
C.
D.
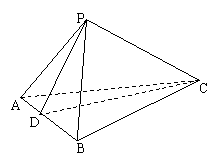
解:
过C作CD⊥AB,连接PD.
由题意PC⊥平面PAB,∴PC⊥AB,∴AB⊥平面PCD.
∴AB⊥PD,
.
,
.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -