| 平面与平面的位置关系 |
主编:黄冈中学数学集体备课组
1.两个平面平行的判定
(1)两个平面平行的定义:如果两个平面没有公共点,则这两个平面平行.
(2)两个平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
注意:这个定理的另外一种表达方式为“如果一个平面内有两条相交直线和另一个平面内的两条相交直线分别平行,那么这两个平面平行”.
(3)平行于同一平面的两个平面互相平行.
2.平面与平面平行的性质
(1)如果两个平面平行,那么其中一个平面内的任意直线均平行于另一个平面.
此结论可以作为定理用,可用来判定线面平行.
(2)两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行.
(3)夹在两个平行平面间的平行线段相等.
3.平面与平面垂直的判定
(1)平面与平面垂直的定义
两个平面相交,如果所成的二面角是直二面角,则称这两个平面互相垂直.
(2)两个平面垂直的判定定理
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
4.平面与平面垂直的性质
(1)两个平面垂直的性质定理
如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
(2)如果两个相交平面都垂直于第三个平面,那么它们的交线垂直于第三个平面.
(3)三个两两垂直的平面的交线两两垂直.
(4)如果两个平面垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内.
5.二面角
(1)二面角的定义
一条直线出发的两个半平面所形成的图形称为二面角,这条直线称为二面角的棱,两个半平面称为二面角的面.
(2)二面角的平面角的定义:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角,叫做二面角的平面角.
注意:①二面角的平面角两边必须都与棱垂直.
②二面角的平面角的大小是由二面角的两个面的位置关系所确定的,与定义中棱上任一点的选择无关,也就是二面角的平面角不只一个,但这些平面角的大小是相等的.
③二面角的平面角的范围是
,当两个半平面重合时
;相交时
;共面时
.平面角是直角的二面角叫做直二面角.
(3)二面角的平面角的确定与求法
①直接法
这种方法的思路是:先作出二面角的平面角,然后通过解三角形,求出平面角的大小,即为所求的二面角的大小.
②公式法
射影面积公式,如果平面多边形的面积为S,它在平面α内的射影面积为
,平面多边形与平面α所夹的锐二面角为θ,那么
.
例1.M、N、P为三个不重合的平面,a、b、c为三条不同直线,则下列命题中,不正确的是( )
①
②
③
④
⑤
⑥
A.④⑥ B.②③⑥
C.②③⑤⑥ D.②③
答案:C
例2.如图所示,已知P为
所在平面外一点,
分别是
的重心.求证:平面
//平面ABC.
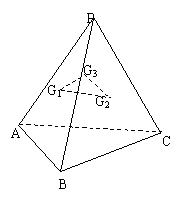
证明:
连接
并延长分别交AB、BC、AC于点D、E、F.
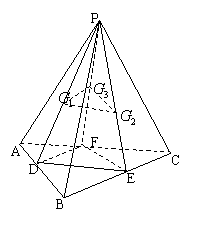
根据重心性质,有
,∴G1G2//DE,G1G3//DF.
∵G1G2∩G1G3=G1,DE∩DF=D.
∴平面G1G2G3//平面ABC.
例3.如图,P是△ABC所在平面外一点,∠ABC=90°,PA=PB=PC,求证:平面PAC⊥平面ABC.
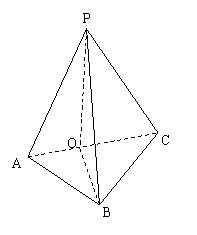
证明:
过P作PO⊥AC,连接OB.
∵PA=PC,∴O为AC的中点,又∵∠ABC=90°,∴OB=OC.
∴△POB≌△POC,∴∠POB=∠POC=90°,即PO⊥OB,又PO⊥OC.
∴PO⊥平面ABC,∵PO
平面PAC,∴平面PAC⊥平面ABC.
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -