(1)请你求出这种切割、焊接而成的长方体的最大容积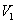 ;
;
(2)由于上述设计存在缺陷(材料有所浪费),请你重新设计切焊方法,使材料浪费减少,而且所得长方体容器的容积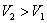 .
.
分析:
设切去正方形边长为x,把体积表示成x的函数,再利用均值不等式.求出最值.
解:
(1)设切去正方形边长为x,则焊接成的长方体的底面边长为4-2x,高为x,
所以 .
.
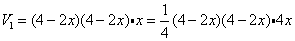
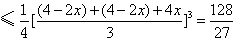 ,
,
当且仅当4-2x=4x,即x=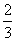 时等号成立.
时等号成立.
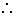 当x=
当x=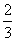 时,
时,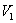 取得最大值
取得最大值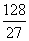 .
.
(2)重新设计方案如图:
如图(c),在正方体的两个角处各切下一个边长为1的小正方体;如图(d),将切下的小正方形焊在未切口的正方形一边的中间;如图(e),将图(d)焊成长方体容器.
新焊长方体容器底面是一长方形,长为3,宽为2,此长方体容积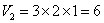 ,
,