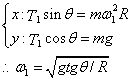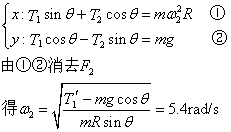| 圆周运动中牛顿运动定律的应用 |
主编:黄冈中学物理集体备课组
一、水平面内的圆周运动
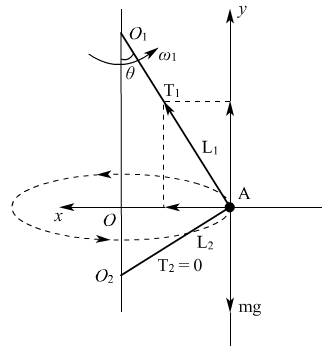
例1、如图所示,用两根分别长L1=4m和L2=3m的细线拴质量为m=2kg的小球A.两细线L1、L2的另一端分别系在竖直杆的O1、O2处.已知O1O2=5m(取g=10m/s2),则
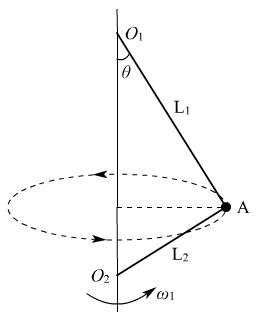
(1)当竖直杆以角速度ω1匀速转动时,O2A线刚好伸直且不受力,求此时角速度ω1的大小;
(2)当O1A线所受的力为100N时角速度ω2的大小.
解:(1)令F2=0
由几何关系θ=37°,
∴ω1≈1.77rad/s
(2)F1′=100N时,F1′cosθ=100×0.8=80牛>mg,故F2≠0
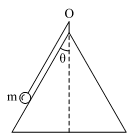
例2、一个光滑的圆锥体固定在水平桌面上,其轴线沿竖直方向,母线与轴线之间的夹角为θ = 30°,如图所示。一长为L的绳(质量不计),一端固定在圆锥体的顶点O处,另一端拴着一个质量为m的小物体(可看做质点)。物体以速度v绕圆锥体的轴线在水平面内做匀速圆周运动。
(1)当v1 =
时,求绳对物体的拉力;
(2)当v2 =
时,求绳对物体的拉力。
解析:
当物体以某一速率绕圆锥体的轴线做水平匀面内的匀速圆周运动时,可能存在圆锥体对物体的弹力为零的临界状况,此时物体刚好与圆锥面接触但不发生形变。而当速率变大时,物体将脱离圆锥面,从而导致绳对物体的拉力大小和方向都要变化。因此,此题的关键是先求出临界状态下线速度的值。
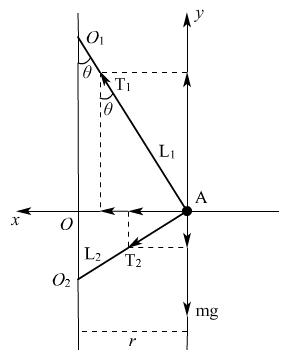
以小物体为研究对象,假设它与圆锥面接触,而没有弹力作用。受力如图甲所示,根据运动定律得:
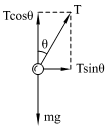
Tcosθ = mg ①
Tsinθ =
②
解①、②得:v =
(1)因为v1 =
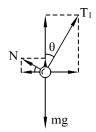
<v ,所以物体m与圆锥而接触且有压力,受力如图乙所示,由运动定律得:
T1cosθ + Nsinθ = mg ③
T1sinθ-Ncosθ = m
④
解③、④得拉力:T1 =
(3
+ 1)
(2)因为v2 =
>v ,所以物体m脱离圆锥面,设绳子与轴线的夹角为φ ,受力如图丙所示,由运动定律得:
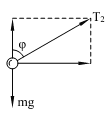
T2sinφ = m
⑤
T2cosφ = mg ⑥
解⑤、⑥得绳子拉力:T2 = 2mg
二、竖直平面内的圆周运动
对于甲图:
方能做圆运动.
乙图
杆上无作用力.
杆上有拉力.
杆上有压力.
例3、如图所示,质量为m的小球固定在长为L的细杆一端,绕细杆的另一端O在竖直面内做圆周运动,球转到最高点A时,线速度大小为
,则( )
A.杆受到
的拉力 B.杆受到
的压力
C.杆受到
的拉力 D.杆受到
的压力
答案:B
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -