1、在竖直平面内作圆周运动的临界问题
（1）如图4－2－2和图4－2－3所示，没有物体支撑的小球，在竖直平面内做圆周运动过最高点的情况：
图4－2－2 图4－2－3
①临界条件：绳子或轨道对小球没有力的作用：mg=m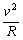
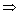v临界=
；
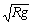②能过最高点的条件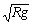：v≥
，当v＞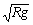
时，绳对球产生拉力，轨道对球产生压力；
③不能过最高点的条件：v＜v临界（实际上球还没到最高点时就脱离了轨道）.
（2）如图4－2－4的球过最高点时，轻质杆对球产生的弹力情况：
①当v=0时，FN=mg（FN为支持力）；
②当0＜v＜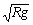
时，FN随v增大而减小，且mg＞FN＞0，FN为支持力；
③当v=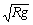
时，FN=0； ④当v＞
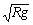时，FN为拉力，FN随v的增大而增大.
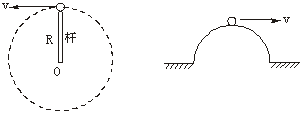
图4－2－4 图4－2－5
若是图4－2－5的小球在轨道的最高点时，如果v≥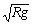
，此时将脱离轨道做平抛运动，因为轨道对小球不能产生拉力.
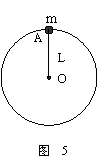
例1、长L＝0.5m，质量可以忽略的的杆，其下端固定于O点，上端连接着一个质量m＝2kg的小球A，A绕O点做圆周运动（同图5），在A通过最高点，试讨论在下列两种情况下杆的受力：
①当A的速率v1＝1m／s时 ②当A的速率v2＝4m／s时
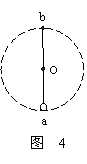
解析：
V0=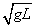
＝
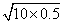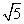m／s＝
m／s
小球的速度大于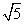
m／s时受拉力，小于
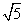m／s时受压力。
解法一：
①当v1＝1m／s＜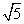
m／s时，小球受向下的重力mg和向上的支持力N
由牛顿第二定律 mg－N＝m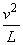
N＝mg－m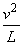
＝16N
即杆受小球的压力16N。
②当v2＝4m／s＞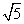
m／s时，小球受向下的
重力mg和向下的拉力F，由牛顿第二定律 mg＋F＝m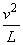 
F＝m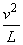 
－mg＝44N
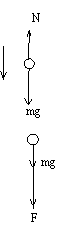
即杆受小球的拉力44N。
解法二：
小球在最高点时既可以受拉力也可以受支持力，因此杆受小球的作用力也可以是拉力或者是压力。我们可不去做具体的判断而假设一个方向。如设杆竖直向下拉小球A，则小球的受力就是上面解法中的②的情形。
由牛顿第二定律 mg＋F＝m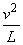
得 F＝m（
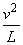－g）
当v1＝1m／s时，F1＝－16N F1为负值，说明它的实际方向与所设的方向相反，即小球受力应向上，为支持力。则杆应受压力。
当v2＝4m／s时，F2＝44N。 F2为正值，说明它的实际方向与所设的方向相同，即小球受力就是向下的，是拉力。则杆也应受拉力。
2、在水平面内作圆周运动的临界问题
在水平面上做圆周运动的物体，当角速度ω变化时，物体有远离或向着圆心运动的（半径有变化）趋势。这时，要根据物体的受力情况，判断物体受某个力是否存在以及这个力存在时方向朝哪（特别是一些接触力，如静摩擦力、绳的拉力等）。
例2、如图6所示，两绳系一质量为m＝0.1kg的小球，上面绳长L＝2m，两端都拉直时与轴的夹角分别为30°与45°，问球的角速度在什么范围内，两绳始终张紧，当角速度为3rad／s时，上、下两绳拉力分别为多大？
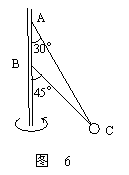
解析：
①当角速度ω很小时，AC和BC与轴的夹角都很小，BC并不张紧。当ω逐渐增大到30°时，BC才被拉直（这是一个临界状态），
但BC绳中的张力仍然为零。设这时的角速度为ω1，则有：
TACcos30°＝mg
TACsin30°＝mω12Lsin30°
将已知条件代入上式解得 ω1＝2.4 rad／s
②当角速度ω继续增大时TAC减小，TBC增大。设角速度达到ω2时，TAC＝0（这又是一个临界状态），则有：TBCcos45°＝mg
TBCsin45°＝mω22Lsin30°
将已知条件代入上式解得 ω2＝3.16 rad／s
所以当ω满足 2.4 rad／s≤ω≤3.16 rad／s，AC、BC两绳始终张紧。
本题所给条件 ω＝3 rad／s，此时两绳拉力TAC、TBC都存在。
TACsin30°＋TBCsin45°＝mω2Lsin30°
TACcos30°＋TBCcos45°＝mg
将数据代入上面两式解得 TAC＝0.27N，TBC＝1.09N
注意：解题时注意圆心的位置（半径的大小）。
如果ω＜2.4 rad／s时，TBC＝0，AC与轴的夹角小于30°。
如果ω＞3.16rad／s时，TAC＝0，BC与轴的夹角大于45°。
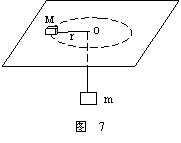
例3、如图7所示，细绳一端系着质量M＝0.6kg的物体，静止在水平面上，另一端通过光滑的小孔吊着质量m＝0.3kg的物体，M的中与圆孔距离为0.2m，并知M和水平面的最大静摩擦力为2N。现使此平面绕中心轴线转动，问角速度ω在什么范围m会处于静止状态？（g＝10m／s2）[先以m＝0为题引入，由浅入深]
解析：
要使m静止，M也应与平面相对静止。而M与平面静止时有两个临界状态：
当ω为所求范围最小值时，M有向着圆心运动的趋势，水平面对M的静摩擦力的方向背离圆心，大小等于最大静摩擦力2N。
此时，对M运用牛顿第二定律。
有T－fm＝Mω12r 且 T＝mg
解得 ω1＝2.9rad／s
当ω为所求范围最大值时，M有背离圆心运动的趋势，水平面对M的静摩擦力的方向向着圆心，大小还等于最大静摩擦力2N。
再对M运用牛顿第二定律有 T＋fm＝Mω22r
解得 ω2＝6.5 rad／s
所以，题中所求ω的范围是： 2.9 rad／s＜ω＜6.5 rad／s
