| 太阳与行星的引力 万有引力定律 |
主编:黄冈中学物理集体备课组
一、太阳与行星的引力
设行星质量为m,太阳质量为M,间距为r.
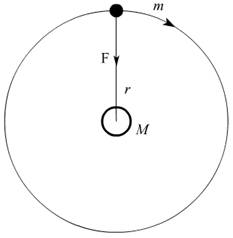
①
②
由①②F=4π2km/r2
可见
由牛顿第三定律,行星对太阳的引力
月地检验:牛顿时代已知月球与地球间距r=60R地
周期T=1个月,g=9.8m/s2,月球的向心加速度
二、万有引力定律
1、内容
2、大小
,G=6.67×10-11Nm2/kg(引力恒量)
3、适用范围:
(1)质点间引力;
(2)质量均匀分布的球体间引力计算.
三、万有引力定律的理解
1、式中G值:相当于两个质量均为1kg,相距1m,其相互引力甚小,只有6.67×10-11N.由于引力恒量太小,这正是牛顿万有引力定律发表一百余年后,英国学者卡文迪许才测定的.
2、定律的应用时具有以下性质:
(1)普遍性;(2)宏观性;(3)相互性.
例1、对于万有引力定律的数学表达式
,下列说法正确的是( )
A.公式中G为引力常量,是人为规定的
B.r趋近零时,万有引力趋于无穷大
C.m1,m2受到的万有引力总是大小相等,与m1,m2的大小无关
D.m1,m2受到的万有引力总是大小相等,方向相反,是一对平衡力
答案:C
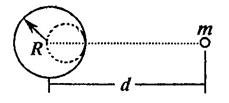
例2、如图所示,一个半径为R、质量为M的均匀球体,紧贴球的边缘挖去一个半径为
的球形后,对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
解析:
完整的均质球体对球外质点m的引力为
,这个引力可以看成是挖去球穴后的剩余部分对质点的引力F1与半径为
的小球对质点的引力F2之和,即F=F1十F2.
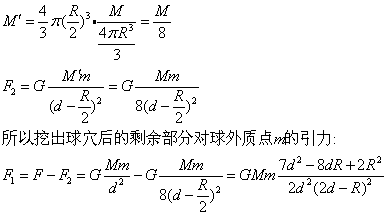
设半径为
的小球质量为M′,则
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -