例1、一物体静置在平均密度为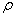 的球形天体表面的赤道上。已知万有引力常量为G,若由于天体自转使物体对天体表面压力恰好为零,则天体自转周期为( )
的球形天体表面的赤道上。已知万有引力常量为G,若由于天体自转使物体对天体表面压力恰好为零,则天体自转周期为( )
A.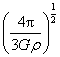 B.
B.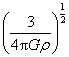
C.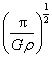 D.
D.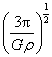
答案:D
解析:
球形天体表面的赤道上,物体对天体表面压力恰好为零,说明天体对物体的万有引力恰好等于物体随天体运动所需的向心力,有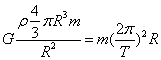 ,解得:
,解得: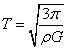 。正确选项为D。
。正确选项为D。
例2、已知地球同步卫星离地面的高度约为地球半径的6倍。若某行星的平均密度为地球平均密度的一半,它的同步卫星距其表面的高度是其半径的2.5倍,则该行星的自转周期约为( )
A.6小时 B. 12小时
C. 24小时 D. 36小时
答案:B
解析:
地球的同步卫星的周期为T1=24小时,轨道半径为r1=7R1,密度ρ1。某行星的同步卫星周期为T2,轨道半径为r2=3.5R2 ,密度ρ2。根据牛顿第二定律和万有引力定律分别有
,密度ρ2。根据牛顿第二定律和万有引力定律分别有
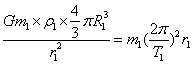
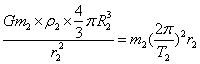
两式化简得T2=T1/2=12小时,选项B正确。
例3、火星直径约为地球的一半,质量约为地球的十分之一,它绕太阳公转的轨道半径约为地球公转半径的1.5倍。根据以上数据,以下说法正确的是( )
A.火星表面重力加速度的数值比地球表面小
B.火星公转的周期比地球的长
C.火星公转的线速度比地球的大
D.火星公转的向心加速度比地球的大
答案:AB
解析:
由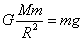 得
得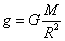 ,计算得火星表面的重力加速度约为地球表面的
,计算得火星表面的重力加速度约为地球表面的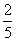 ,A正确;由
,A正确;由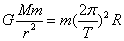 得
得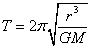 ,公转轨道半径大的周期长,B对;周期长的线速度小,(或由
,公转轨道半径大的周期长,B对;周期长的线速度小,(或由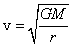 判断轨道半径大的线速度小),C错;公转向心加速度
判断轨道半径大的线速度小),C错;公转向心加速度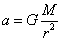 ,D错。
,D错。