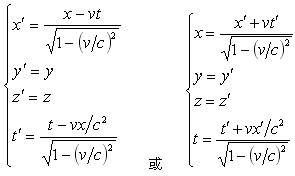
据狭义相对论的两个基本假设来推导洛仑兹变换式。
1、时空坐标间的变换关系
作为一条公设，我们认为时间和空间都是均匀的，因此时空坐标间的变换必须是线性的。
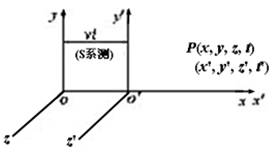
对于任意事件P在S系和S′系中的时空坐标(x，y，z，t)、(x′，y′，z′，t′)，因S′相对于S以平行于x轴的速度v作匀速运动，显然有y′=y, z′=z。
在S系中观察S系的原点，x=0；在S′系中观察该点，x′=-vt′，即x′+vt′=0。因此x=x′+vt′。
在任意的一个空间点上，可以设：x=k（x′+vt′），k是—比例常数。
同样地可得到：x′=k′（x-vt）= k′（x+(-v)t）
根据相对性原理，惯性系S系和S′系等价，上面两个等式的形式就应该相同（除正、负号），所以k=k′。
2. 由光速不变原理可求出常数k
设光信号在S系和S′系的原点重合的瞬时从重合点沿x轴前进，那么在任一瞬时t（或t′），光信号到达点在S系和S′系中的坐标分别是：x=ct, x′=ct′，则：
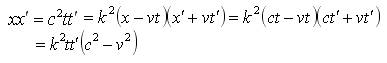
由此得到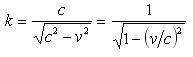
。
这样，就得到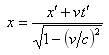
，
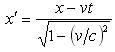。由上面二式，消去x′得到
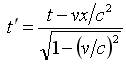；若消去x得到
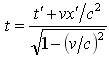，综合以上结果，
就得到洛仑兹变换，或洛仑兹反变换
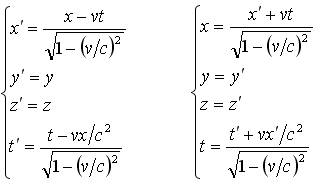
可见洛仑兹变换是两条基本原理的直接结果。
3、讨论
（1）可以证明，在洛仑兹变换下，麦克斯韦方程组是不变的，而牛顿力学定律则要改变。故麦克斯韦方程组能够用来描述高速运动的电磁现象，而牛顿力学不适用描述高速现象，故它有一定的适用范围。
（2）当|v/c|<<1时，洛仑兹变换就成为伽利略变换，亦即后者是前者在低速下的极限情形。故牛顿力学仅是相对论力学的特殊情形—低速极限。
