| 探索弹性势能的表达式 |
主编:黄冈中学物理集体备课组
一、弹力做功
弹簧的弹力是变力,我们能否利用恒力做功公式W=Flcosα计算弹簧弹力做的功呢?
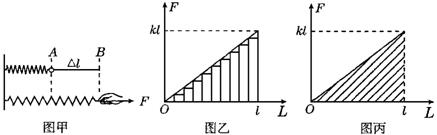
可以,首先应将变力转化为恒力,如图甲所示,缓缓拉动弹簧,使弹簧伸长l,把拉伸弹簧的过程分为很多小段,拉力在每小段可以认为是恒力,它在各段做功之和可以代表拉力在整个过程做的功.
弹簧从A拉伸到B的过程被分成很多小段,它们的长度是
△l1,△l2,△l3,…
在各个小段上,拉力可以近似认为是不变的,它们分别是
F1,F2,F3,…
在各个小段上,拉力做的功分别是
F1△l1,F2△l2,F3△l3,…
拉力在整个过程中做的功可以用它在各小段做功之和来代表:
WF=F1△l1+F2△l2+F3△l3+…
在F—l图像中,F1△l1,F2△l2,F3△l3,…是一系列矩形的面积,故此和为图乙中一系列矩形面积之和.当△l1,△l2,△l3,…各小段分割得越来越小时,这些矩形面积的和就越来越接近图丙所示的三角形面积.
故弹簧的弹力做的功就为
方法二(平均值法):
由胡克是律F=kl可知,弹簧的弹力F跟形变量l成正比(线性关系),所以弹力做的功也可以用平均力
去求,故有
注意:这种求平均值的方法只适用于线性函数关系,若F与l是二次函数关系则不能用这种求算术平均值的方法计算平均力.
二、弹性势能
1、定义:发生弹性形变的物体的各部分之间,由于有相互作用的弹力,也具有势能,这种势能叫做弹性势能。
2、当弹簧的长度为原长时,它的弹性势能为零,弹簧被拉长或压缩后,就具有了弹性势能。
例1、关于弹性势能,下列说法中正确的是( )
A.任何发生弹性形变的物体,都具有弹性势能
B.任何具有弹性势能的物体.一定发生了弹性形变
C.物体只要发生形变,就一定具有弹性势能
D.弹簧的弹性势能只跟弹簧被拉伸或压缩的长度有关
解析:
由弹性势能的定义和相关因素进行判断.发生弹性形变的物体的各部分之间,由于弹力作用而能对别的物体做功.而具有的势能,叫做弹性势能.所以,任何发生弹性形变的物体都具有弹性势能,任何具有弹性势能的物体一定发生了弹性形变.物体发生了形变,若是非弹性形变,不能对外做功,无弹力作用,则物体就不具有弹性势能.弹簧的弹性势能除了跟弹簧被拉伸或压缩的长度有关外,还跟弹簧劲度系数的大小有关.正确选项为A、B.
答案:AB
例2、关于弹簧的弹性势能,下列说法中正确的是(规定弹簧处于自然长度时的弹性势能为零)( )
A.当弹簧变长时,它的弹性势能一定增大
B.当弹簧变短时,它的弹性势能一定变小
C.在拉伸长度相同时,越大的弹簧,它的弹性势能越大
D.弹簧在拉伸时的弹性势能一定大于压缩时的弹性势能
提示:
①弹簧弹性势能大小与什么因素有关?
②
中的l代表什么?是弹簧的长度吗?
答案:C
三、弹力做功与弹性势能的关系
1、弹力做功可由F—l图象下的“面积”求解或由平均力求解。
2、弹性势能的改变仅与弹力做功有关,弹力对外做多少正功,弹性势能就能减少多少;弹力对外做多少负功,弹性势能就增加多少.即W弹=-△E弹
例3、如图所示,在光滑水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F的作用下物体处于静止状态,当撤去F后,物体将向右运动。在物体向右运动的过程中,下列说法正确的是( )
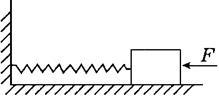
A.弹簧的弹性势能逐渐减小
B.弹簧的弹性势能逐渐增大
C.弹簧的弹性势能先增大后减小
D.弹簧的弹性势能先减小后增大
解析:
由物体处于静止状态可知,弹簧处于压缩状态,撤去F物体在向右运动的过程中,弹簧的弹力对物体先做正功后做负功,故弹簧的弹性势能应先减少后增大。
答案:D
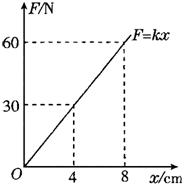
例4、一根弹簧的弹力F一形变量x图线如图所示,那么弹簧由伸长量8cm到伸长量4cm的过程中,弹力功和弹性势能的变化量为( )
A.3.6 J,-3.6J B.-3.6J,3.6J
C.1.8J,-1.8J D.-1.8J,1.8J
①由F—x图象下的面积求弹力功.
②弹簧伸长量变小,弹力做正功还是负功?弹性势能如何变化?
答案:C
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -