例1、一质点开始时做匀速直线运动，从某时刻起受到一恒力作用．此后，该质点的动能可能( )
A．一直增大
B．先逐渐减小至零，再逐渐增大
C．先逐渐增大至某一最大值，再逐渐减小
D．先逐渐减小至某一非零的最小值，再逐渐增大
答案：ABD
解析：
当所加恒力的方向与物体运动的方向成锐角时，该力一直做正功，其动能一直增大，A正确；当所加恒力的方向与物体运动的方向相反时，物体先做匀减速运动后做反向的匀加速运动，其动能先逐渐减小至零，再逐渐增大，B正确；当所加恒力的方向与物体运动的方向成钝角(不等于180°)时，其动能先逐渐减小至某一非零的最小值，再逐渐增大，D正确；物体不可能出现动能先逐渐增大至某一最大值，再逐渐减小的情况，C错误．
例2、如图所示，以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑水平地面上，左端紧靠B点，上表面所在平面与两半圆分别相切于B、C。一物块被轻放在水平匀速运动的传送带上E点，运动到A时刚好与传送带速度相同，然后经A沿半圆轨道滑下，再经B滑上滑板。滑板运动到C时被牢固粘连。物块可视为质点，质量为m，滑板质量M=2m，两半圆半径均为R，板长l =6.5R，板右端到C的距离L在R＜L＜5R范围内取值。E距A为S=5R，物块与传送带、物块与滑板间的动摩擦因素均为μ=0.5，重力加速度取g.
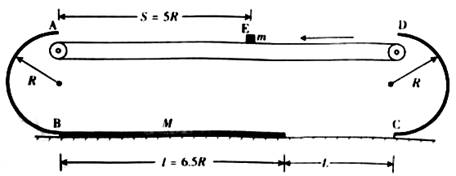
（1）求物块滑到B点的速度大小；
（2）试讨论物块从滑上滑板到离开滑板右端的过程中，克服摩擦力做的功Wf与L的关系，并判断物块能否滑到CD轨道的中点。
解析：
（1）μmgs＋mg·2R=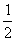
mvB2 ①
所以 vB=3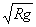
（2）设M滑动x1，m滑动x2二者达到共同速度v，则
mvB=(M＋m)v ②
μmgx1=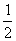
mv2 ③
—μmgx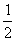2=
mv2—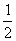
mvB2 ④
由②③④得v=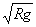
，x1=2R，x2=8R
二者位移之差△x= x2—x1=6R＜6.5R，即滑块未掉下滑板
讨论：
①R＜L＜2R时，Wf=μmg(l＋L)=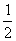 
mg（6.5R＋L）
②2R≤L＜5R时，Wf=μmgx2+μmg(l—△x)=4.25mgR＜4.5mgR，即滑块速度不为0，滑上右侧轨道。
要使滑块滑到CD轨道中点，vc必须满足：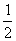
mvc2 ≥mgR ⑤
此时L应满足：μmg(l+L) ≤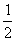
mvB2—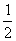
mvc2 ⑥
则L≤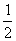
R，不符合题意，滑块不能滑到CD轨道中点。
答案：
（1） vB=3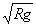
（2）①R＜L＜2R时，Wf=μmg(l＋L)=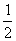 
mg（6.5R＋L）
②2R≤L＜5R时，Wf=μmgx2+μmg(l—△x)=4.25mgR＜4.5mgR，即滑块速度不为0，滑上右侧轨道，滑块不能滑到CD轨道中点.
