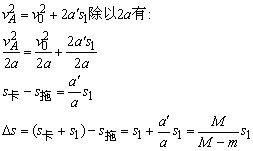| 动能和动能定理(二) |
主编:黄冈中学物理集体备课组
应用动能定理解题的基本步骤:
1、受力分析,画出物体的受力示意图.
2、分析每个力做功的情况.
3、选定研究过程,根据动能定理列方程.
4、解方程并讨论结果.
例1、如图,在一倾角为30°的斜坡上,一辆汽车从A点由静止出发后开始爬坡,在牵引力不变的条件下,行进45m到达B点,此后,司机关掉油门,汽车又前进了15m停在C点,汽车与路面的摩擦因数
,汽车质量m=104kg,g=10m/s2.求:
(1)汽车在AB段的牵引力;
(2)汽车经过B点时的速度.

解:
(1)汽车受力如图所示,则有
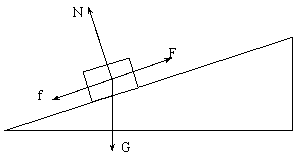
f=μN=μmgcos30°=
对全过程应用动能定理,有
F·sAB-(f+mgsin30°)·sAC=0
(2)设汽车在B点的速度为vB,对B→C的过程应用动能定理,有
-(f+mgsin30°)·sBC=0-
例2、一辆带着拖车的卡车总质量为M,沿平直公路匀速前进,在途中质量为m的拖车脱钩,当司机发觉时,卡车已驶过脱钩点s1,于是立即关闭油门,若阻力与车重成正比,且关闭油门前卡车的牵引力不变,试求卡车和拖车都静止时,两车之间的距离.
解法一:
对整体有:F=kMg ①
设脱钩后拖车的位移为s,卡车的位移为s′
对拖车和卡车全过程分别应用动能定理,有
-kmgs=0-
②
Fs1-k(M-m)gs′=0-
③
由①②③,得
(M-m)(s′-s)=Ms1
解法二:
关闭油门后:a=kg
未关闭油门时,F合=0,则有
ma=(M-m)a′
对系统用牛顿第二定律
设卡车加速的最大速度为vA,则有
解法三:
若拖车脱钩后卡车也无牵引力,则s相同,由此可见拖车多前进的距离也就是由于牵引力F=kMg在位移s1上多做的功,则有
kMgs1=k(M-m)g·△s
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -