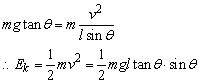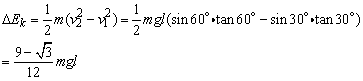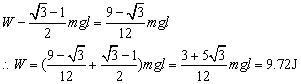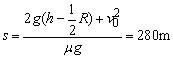| 动能和动能定理(三) |
主编:黄冈中学物理集体备课组
一、求变力做功
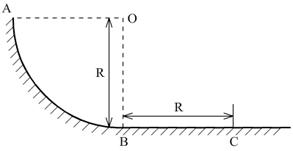
例1、如图,用同样材料制成的一个轨道,AB段为
圆弧,半径为R,水平放置的BC段长为R,一小物块质量为m,与轨道间动摩擦因数为μ,当它从轨道顶端A由静止下滑时恰好运动到C点静止,那么,物块在AB段克服摩擦力所做的功为__________.
解:
从A到C的过程,根据动能定理有mgR-Wf-μmgR=0
故克服摩擦力做功Wf=(1-μ)mgR
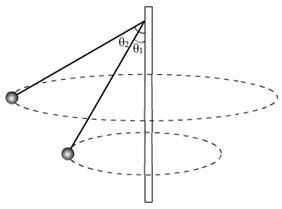
例2、如图,OA是由机器带动绕其轴线旋转的竖直杆,细绳的一端固定在杆的A端,另一端系一质量为m=1kg的小球,绳长l=1m,开始时小球绕轴线在水平面内做匀速圆周运动,细绳与竖直杆间夹角θ1=30°,现使机器转速加大,使小球在另一水平面内做稳定的匀速圆周运动时,细绳与竖直杆间夹角θ2=60°.求此过程中绳子的拉力对小球所做的功.
解:
小球在水平面内做匀速圆周运动
向心力由重力和拉力的合力提供,则有
θ角由30°增大到60°的过程中,动能增量为
此过程中重力做的功为
设绳子拉力做的功为W,由动能定理,可知
总结求变力做功的方法:
1、平均值法.
2、示功图.
3、动能定理.
二、周期性的往复运动
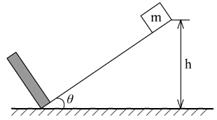
例3、如图,质量为m的滑块放在倾角为θ的斜面上,与斜面间的动摩擦因数为μ,让滑块从斜面上高为h的地方无初速滑上,在斜面底端与固定挡板P相撞,碰撞时无动能损失,m以碰撞前的速度反弹,滑到最高点后再滑回来碰撞挡板,如此反复.问从释放到滑块最终停止,在斜面上通过的总路程为多少?
解:
滑块最终紧靠P停止,设通过的总路程为s,全过程应用动能定理,有
mg-μmgcosθ·s=0
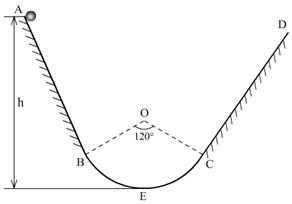
例4、如图,AB与CD为两个对称斜面,其上部足够长,下部分别与一个光滑的圆弧面的两端相切,圆弧圆心角为120°,半径R为2.0m,一个物体在离弧底E高度为h=3.0m处,以初速度4.0m/s沿斜面运动.若物体与两斜面的动摩擦因数为0.02,则物体在两斜面上(不包括圆弧部分)一共能走多长路程?(g取10m/s2).
解:
设物体在斜面上运动的总路程为s,则摩擦力所做的总功为-μmgs·cos60°.
对全过程由动能定理,得
mg[h-R(1-cos60°)]-μmgcos60°=0-
物体在斜面上通过的总路程为
小结:
处理周期性的往复运动时应注意分析:①物体的初状态和末状态的特点,主要指位置和速度;②物体运动过程中各个力所做的功;③根据动能定理列方程并求解.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -