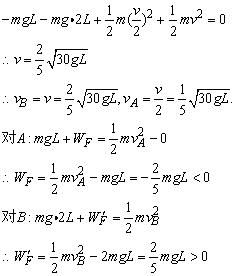| 机械能守恒定律(一) |
主编:黄冈中学物理集体备课组
自由落体和竖直上抛说明动能和重力势能可相互转化,初中也学过动能和弹性势能也能相互转化.
一、概念
1、机械能:动能和势能(弹性势能和重力势能)统称为机械能.
E=Ek+Ep
分析和复习Ek、Ep的特点.
2、动能与势能的相互转化
①重力势能→动能.
②动能→重力势能.
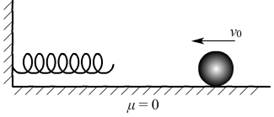
③动能→弹性势能.
④弹性势能→动能.
二、机械能守恒定律
1、理论推导
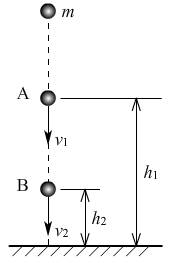
从B→C的过程,由动能定理,有
①
根据重力做功与重力势能的关系,有
WG=-△Ep=mgh1-mgh2 ②
由①②,得
即Ek2+Ep2=Ek1+Ep1
2、内容:在只有重力和弹力做功的情形下,物体的动能和势能发生相互转化,但机械能的总量保持不变.
3、表达形式
①Ek1+Ep1=Ek2+Ep2
②△Ek=-△Ep
③△Ek+△Ep=0
4、守恒条件
①只有重力和弹力做功.
②其他的外力和内力不做功或做功之和为零.
5、证明
①前面利用自由落体运动推导.
②利用平抛运动证明.
设一个质量为m的物体以水平速度v0抛出,下落高度为h时,速度为v,由平抛运动的知识可知,
即v2=v02+2gh ①
选抛出点为零势能参考面,物体开始时的机械能为
②
物体下落h高度时机械能为E2=
mv2-mgh ③
①代入③,得
∴E1=E2,机械能守恒.
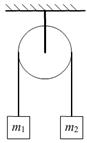
例1、如图,一轻绳跨过定滑轮悬挂质量为m1,m2的两个物体,滑轮质量及所有摩擦均不计,m1<m2,系统由静止开始运动的过程中,(m1未跨过滑轮)
A.m1,m2各自的机械能分别守恒
B.m2减少的机械能等于m1增加的机械能
C.m2减少的重力势能等于m1增加的重力势能
D.m1,m2组成的系统机械能守恒
答案:BD
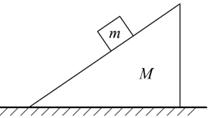
例2、如图所示,斜面置于光滑的水平地面上,光滑斜面上有一物体由静止沿斜面下滑,在物体下滑过程中下列说法正确的是( )
A.物体的重力势能减少,动能增大
B.物体的机械能不变
C.物体与斜面间弹力对斜面不做功
D.物体与斜面组成的系统机械能守恒
答案:AD
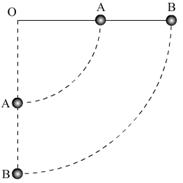
例3、水平轻质杆固定于O点且可绕O点在竖直平面内自由转动,水平杆长2l,另一端及中点各有一个质量为m的小球A和B,如图所示,当杆由水平位置无初速释放,运动至竖直位置的过程中( )
A.杆OA对小球A不做功
B.杆AB对小球A不做功
C.杆AB对小球做负功
D.杆AB对小球B做负功
分析:
杆OA不做功,只有重力做功,机械能守恒,以过O点的水平面为零势能面,由机械能守恒,
∴AB杆对A做负功,对B做正功.
答案:AC
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -