| 机械能守恒定律(二) |
主编:黄冈中学物理集体备课组
一、应用机械能守恒定律解题的步骤
1、受力分析,画受力示意图.
2、分析物体的运动过程,判断机械能是否守恒.
3、在守恒过程中利用机械能守恒定律写方程.
4、解方程并讨论.
二、实例分析
例1、如图,置于光滑水平面上的小车质量为M,小球质量为m,悬线长为l,开始时将细线拉直成水平,且车、球均静止,自由释放小球后,设小球向下摆到最低点时速度为v,则( )
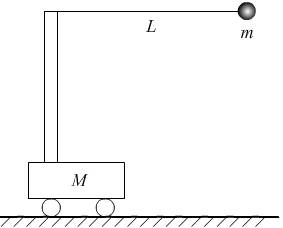
A.
B.
C.
D.无法判断v与
的大小关系
答案:C
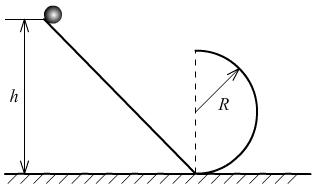
例2、一质量m=2kg的小球从光滑斜面上高h=3.5m处由静止滑下,斜面的底端连着一个半径R=1m的光滑圆环.求:
(1)小球滑至圆环顶点时对环的压力;
(2)小球至少应从多高处静止滑下才能越过圆环最高点.
解:
(1)对小球,从开始运动至圆环顶点的过程中,由机械能守恒定律,有
mgh=
mv2+mg·2R ①
在圆环顶点处,有
②
由①②,得
N=40N
(2)若小球恰好越过圆环顶点,则
③
由①③,得
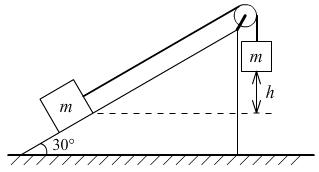
例3、一倾角为30°的固定光滑斜面顶端有一定滑轮,用一轻绳经过定滑轮两端各系一个质量均为m的物体.如图,开始时两物体高度差为h,两物体由静止释放,当两物达同一高度时,它们速度的大小是多少?
解:
两物体在竖直方向的位移分别为hx和hx·sin30°,由几何关系,有
hx+hx·sin30°=h ①
设两物达同一水平面为参考平面,由机械能守恒定律,有
mghx-mghx·sin30°=
·2m·v2 ②
由①②,得
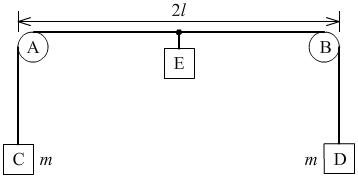
例4、如图,轻质长绳水平地跨在相距为2l的两个小定滑轮A、B上,质量为m的物块E悬挂质量为m的物块C、D,先托住物块E,使绳处于水平拉直状态,静止释放物块E,在物块下落过程中.
(1)当物块E下落距离h为多大时,物块的加速度为零?
(2)物块E下落上述距离的过程中,C、D、E的总动能是多少?
(3)求物块E下落的最大距离.
解:
(1)h=l·tan30°=
(2)物块E下落h时,有C、D上升h′,
△Ep=2mgh′-mgh=(
-2)mgh
△Ek=-△Ep=(2-
)mgh
(3)设物块E下落的最大距离为H,则
mgH-2mg(
-l)=0
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -