| 机械能守恒定律(三) |
主编:黄冈中学物理集体备课组
一、圆周运动的问题
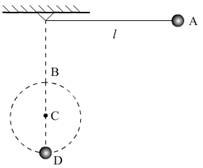
例1、在固定于O点的一根绳子的下端,系一个质量为m的小球,绳长为l,绳子承受的最大拉力为7mg,在离O点h处钉一枚钉子C,把绳拉到水平.如图,释放后,小球到达最低点后以C为圆心做圆周运动,试求h的值.
解:
小球由A点释放,并能绕C点做圆周运动,在运动过程中只有重力做功,故机械能守恒,以O点所在平面为参考面,有
-mghAB=0 ①
在B点:T+mg=
②
R=l-h ③
hAB=h-R=2h-l ④
由①②③④,得
⑤
由于T≥0,由⑤式可知:5h-3l≥0
即
⑥
从A→D的过程,由机械能守恒有
-mgL=0 ⑦
在D点:Tm-mg=
⑧
由③⑦⑧,得
⑨
由⑥⑨,得
二、与弹簧有关的问题
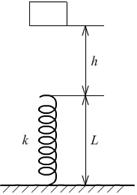
例2、如图,一质量为m的物块位于一质量可忽略的直立弹簧上方h高度处,该物块从静止开始落向弹簧.设弹簧的长度为L,劲度系数为k,以地面为零势面,则下列判断正确的是( )
A.物块获得最大动能时,重力势能为mgL
B.物块获得了大动能时,重力势能为
C.在物块与弹簧接触,到脱离弹簧弹回的过程中,物块所受合外力的功等于零
D.物块获得最大动能时,重力势能等于mg(L-xm),其中xm是弹簧的最大压缩量
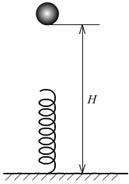
例3、如图,一根轻质弹簧竖直固定在水平地面上,一质量为m的小球自弹簧正上方离地面高度为H1处自由下落,并压缩弹簧,设速度达到最大时的位置离地面的高度为h1,最大速度为v1,若此小球从离地面高度为H2(H2>H1)处自由下落,并压缩弹簧,设速度达到最大时的位置离地面的高度为h2,最大速度为v2,不计空气阻力,则( )
A.v1<v2,h1=h2 B.v1<v2,h1<h2
C.v1=v2,h1<h2 D.v1<v2,h1>h2
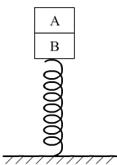
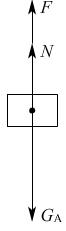
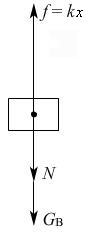
例4、A、B两个木块叠放在竖直轻弹簧上.如图,已知木块A、B的质量分别为0.42kg和0.40kg,轻弹簧的劲度系数k=100N/m,若在木块A上作用一个竖直向上的力F,使木块A由静止开始以0.5m/s2的加速度竖直向上做匀加速运动.(g=10m/s2)
(1)使木块A竖直向上做匀加速运动过程中,力F的最大值是多少?
(2)若木块A由静止开始做匀加速运动,直到与B分离的过程中,弹簧的弹性势能减小了0.248J,求在这个过程中,力F对木块做的功是多少?
解:分析A、B两个物体的受力情况及力的大小变化.
(1)对A:
F+N-mAg=mAa ①
当N=0时F最大,
∴Fmax=mA(g+a)=0.42×(10+0.5)N=4.41N
(2)对B:
kx-N-mBg=mBa ②
开始静止时x1=
=8.2×10-2m
当N=0时,由②式x2=
=4.2×10-2m
A、B分离时的位移S=x1-x2=4.0×10-2m
∴v2=2as=4.0×10-2m2/s2
由动能WF+Wf+WG=
(mA+mB)v2
其中WG=-(mA+mB)g(x1-x2),Wf=-△Ep=0.248J
∴WF=9.6×10-2J
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -