| 运动的合成分解的应用 |
主编:黄冈中学物理集体备课组
一、绳拉物体模型
例1、在一光滑水平面上放一个物体,人通过细绳跨过高处的定滑轮拉物体,使物体在水平面上运动,人以大小不变的速度v运动.当绳子与水平方向成θ角时,物体前进的瞬时速度是多大?
命题意图:考查分析综合及推理能力,B级要求.
错解分析:
弄不清合运动与分运动概念,将绳子收缩的速度按图所示分解,从而得出错解v物=v1=vcosθ.
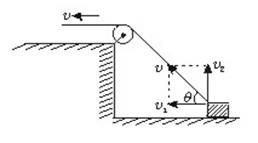
解法一:应用合运动与分运动的关系
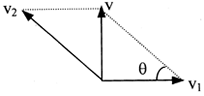
绳子牵引物体的运动中,物体实际在水平面上运动,这个运动就是合运动,所以物体在水平面上运动的速度v物是合速度,将v物按如图所示进行分解.
其中:v=v物cosθ,使绳子收缩.
v⊥=v物sinθ,使绳子绕定滑轮上的A点转动.
所以v物=
解法二:应用微元法
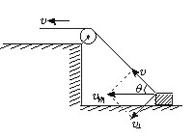
设经过时间Δt,物体前进的位移Δs1=BC,如图所示.过C点作CD⊥AB,当Δt→0时,∠BAC极小,在△ACD中,可以认为AC=AD,在Δt时间内,人拉绳子的长度为Δs2=BD,即为在Δt时间内绳子收缩的长度.
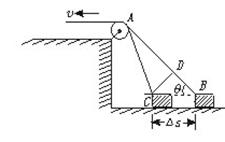
由图可知:BC=
①
由速度的定义:物体移动的速度为v物=
②
人拉绳子的速度v=
③
由①②③解之:v物=
例2、A、B质量均为m,且分别用轻绳连接跨过定滑轮,不计一切摩擦力.当用水平力F拉物体B沿水平方向向右做匀速直线运动过程中( )
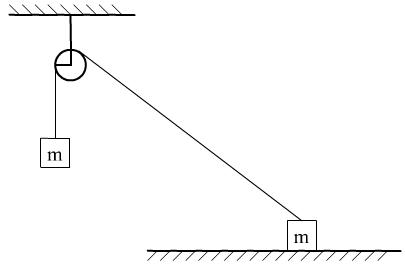
A.物体A也做匀速直线运动
B.绳子拉力始终大于物体A所受重力
C.物体A的速度小于物体B的速度
D.地面对物体B的支持力逐渐增大
分析:
设物体B匀速速度为v,物体B的运动使绳子参与两种分运动:绳子沿定滑轮为圆心垂直于绳子转动,另一分运动是沿绳伸长的分运动,合运动就是物体以速度v向右匀速直线运动.
v1=vsinθ θ↓ sinθ↓ v1↓
vA=v2=vcosθ θ↓ cosθ↑ v2↑ 物体A作变加速运动
对B:Ty+N=mg
开始时N<mg,当B运动至无穷远处时Ty∝0,N=mg
∴地面对物体B的支持力逐渐增大.
例3、两光滑环AB用不可伸长的轻绳相连,当线与竖直方向夹角为
时,此时vA=4m/s, 求B沿杆方向的速度.
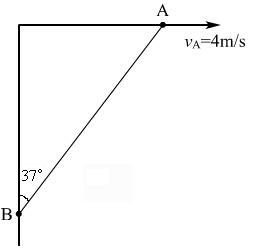
vBcos37°=vAcos53°
二、小船渡河模型
一条宽为d的河流,河水流速为v1,船在静水中速度为v2.
(1)要使船划到对岸时间最短,船头应指向什么方向?最短时间为多少?
(2)要使船划对对岸的航程最短,船头指向什么方向?最短航程是多少?
解:
①设船头斜向上游与河岸成θ角,这时船速v船在y方向的分量为v2′=v船sinθ=v2sinθ,渡河时间为
.
可见,在河宽d和船速v2一定情况下,渡河驶向对岸的时间t随sinθ的增大而减小.当θ=90°时,sinθ=1(最大),即船头与河岸垂直时,渡河时间最短,且tmin=
.
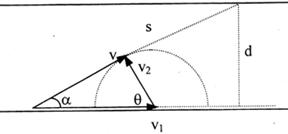
②求航程最短问题应根据v1和v2的大小关系分成以下三种情况讨论:
(i)当v2>v1时,即船头斜向上游与岸夹角为θ,船的合速度可垂直于河岸,航程最短为d,此时沿水流方向合速度为零.
v2cosθ=v1
即船头斜指向上游,与河岸夹角
,船航线就是位移d.
渡河时间
(ii)当v2<v1时,由于船在静水中的速度v2小于水流速度v1,则无论船头驶向何方,总被水流冲向下游,怎样使船所走航线的位移最短呢?虽然位移不可能垂直河岸,但当位移越靠近垂直河岸的方向,位移越短,
,船头与水平方向上游夹角
,最短航程
,所花时间
.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -