指物拉绳(杆)或绳(杆)拉物问题。由于高中研究的绳都是不可伸长的,杆都是不可伸长和压缩的,即绳或杆的长度不会改变,所以解题原则是:把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相同求解。
合速度方向:物体实际运动方向
分速度方向:沿绳(杆)伸(缩)方向:使绳(杆)伸(缩)
垂直于绳(杆)方向:使绳(杆)转动
速度投影定理:不可伸长的杆或绳,若各点速度不同,各点速度沿绳方向的投影相同。
这类问题也叫做:斜拉船的问题——有转动分速度的问题
例题1、如图所示,人用绳子通过定滑轮以不变的速度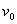 拉水平面上的物体A,当绳与水平方向成θ角时,求物体A的速度。
拉水平面上的物体A,当绳与水平方向成θ角时,求物体A的速度。
★解析:
解法一(分解法):本题的关键是正确地确定物体A的两个分运动。物体A的运动(即绳的末端的运动)可看作两个分运动的合成:一是沿绳的方向被牵引,绳长缩短。绳长缩短的速度即等于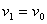 ;二是随着绳以定滑轮为圆心的摆动,它不改变绳长,只改变角度θ的值。这样就可以将
;二是随着绳以定滑轮为圆心的摆动,它不改变绳长,只改变角度θ的值。这样就可以将 按图示方向进行分解。所以
按图示方向进行分解。所以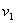 及
及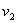 实际上就是
实际上就是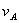 的两个分速度,如图所示,由此可得
的两个分速度,如图所示,由此可得
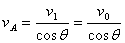 。
。
解法二(微元法):要求船在该位置的速率即为瞬时速率,需从该时刻起取一小段时间来求它的平均速率,当这一小段时间趋于零时,该平均速率就为所求速率。
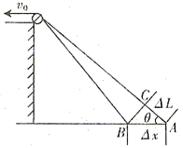
设船在θ角位置经△t时间向左行驶△x距离,滑轮右侧的绳长缩短△L,如图所示,当绳与水平方向的角度变化很小时,△ABC可近似看做是一直角三角形,因而有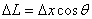 ,两边同除以△t得:
,两边同除以△t得:
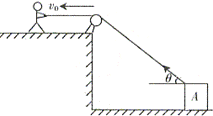
即收绳速率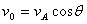 ,因此船的速率为:
,因此船的速率为:
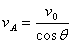
总结:“微元法”。可设想物体发生一个微小位移,分析由此而引起的牵连物体运动的位移是怎样的,得出位移分解的图示,再从中找到对应的速度分解的图示,进而求出牵连物体间速度大小的关系。
解法三(能量转化法):由题意可知:人对绳子做功等于绳子对物体所做的功。人对绳子的拉力为F,则对绳子做功的功率为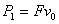 ;绳子对物体的拉力,由定滑轮的特点可知,拉力大小也为F,则绳子对物体做功的功率为
;绳子对物体的拉力,由定滑轮的特点可知,拉力大小也为F,则绳子对物体做功的功率为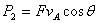 ,因为
,因为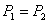 所以
所以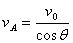 。
。
评点:①在上述问题中,若不对物体A的运动认真分析,就很容易得出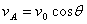 的错误结果;②当物体A向左移动,θ将逐渐变大,
的错误结果;②当物体A向左移动,θ将逐渐变大, 逐渐变大,虽然人做匀速运动,但物体A却在做变速运动。
逐渐变大,虽然人做匀速运动,但物体A却在做变速运动。
总结:解题流程:①选取合适的连结点(该点必须能明显地体现出参与了某个分运动);②确定该点合速度方向(物体的实际速度为合速度)且速度方向始终不变;③确定该点合速度的实际运动效果从而依据平行四边形定则确定分速度方向;④作出速度分解的示意图,寻找速度关系。
例题2、如图所示,在高为H的光滑平台上有一物体.用绳子跨过定滑轮C,由地面上的人以均匀的速度v0向右拉动,不计人的高度,若人从地面上平台的边缘A处向右行走距离s到达B处,这时物体速度多大?物体水平移动了多少距离?
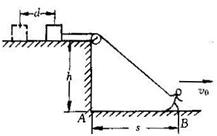
★解析:
人的实际运动为合运动,将此合运动分解在沿绳方向和垂直于绳的方向。
[全解]设人运动到B点时,绳与地面的夹角为θ。人的运动在绳的方向上的分运动的速度为: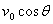 。物体的运动速度与沿绳方向的运动速度相同,所以物体的运动速度为
。物体的运动速度与沿绳方向的运动速度相同,所以物体的运动速度为
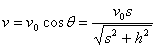 。
。
物体移动的距离等于滑轮右端绳子伸长的长度,
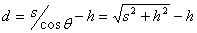 。
。
答案: ,
,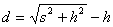
[小结]分清合运动是关键,合运动的重要特征是,合运动都是实际的运动,此题中,人向前的运动是实际的运动,是合运动;该运动分解在沿绳的方向和垂直于绳的方向,这两个运动的物理意义是明确的,从滑轮所在的位置来看,沿绳的方向的运动是绳伸长的运动,垂直于绳的方向的运动是绳绕滑轮的转动,人同时参与了这两个运动,其实际的运动(合运动)即是水平方向的运动
例题3、如图所示,重物M沿竖直杆下滑,并通过绳带动小车m沿斜面升高.问:当滑轮右侧的绳与竖直方向成θ角,且重物下滑的速率为v时,小车的速度为多少?
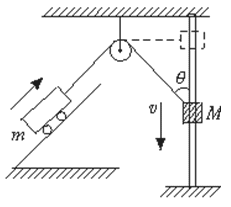
★解析:
方法一:虚拟重物M在Δt时间内从A移过Δh到达C的运动,如图(1)所示,这个运动可设想为两个分运动所合成,即先随绳绕滑轮的中心轴O点做圆周运动到B,位移为Δs1,然后将绳拉过Δs2到C.
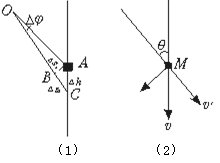
若Δt很小趋近于0,那么Δφ→0,则Δs1=0,又OA=OB,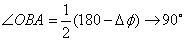 .
.
亦即Δs1近似⊥Δs2,故应有:Δs2=Δh·cosθ
因为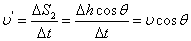
所以v′=v·cosθ
方法二:重物M的速度v的方向是合运动的速度方向,这个v产生两个效果:一是使绳的这一端绕滑轮做顺时针方向的圆周运动;二是使绳系着重物的一端沿绳拉力的方向以速率v′运动,如图(2)所示,由图可知,v′=v·cosθ.