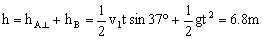例1、如图1所示,斜面倾角为θ,小球从斜面上的A点以初速度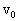 水平抛出,设斜面足够长.从抛出开始算起,求:小球何时离开斜面的距离最大?此时小球的速度是多少?
水平抛出,设斜面足够长.从抛出开始算起,求:小球何时离开斜面的距离最大?此时小球的速度是多少?
解法一:
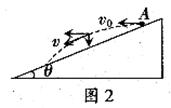
设经过t时间小球离斜面的距离最大,此时小球的速度方向与斜面平行(如图2),则此球的竖直分速度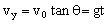 ,则
,则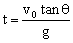 ,此时小球的速度为
,此时小球的速度为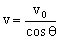 。
。
点评:本解析是抓住了题目的隐含条件——小球瞬时速度与斜面平行时球距斜面最远,然后再按习惯方式把平抛运动沿水平方向和竖直方向分解,这样得到的分运动比较简单.
解法二:
本题参考面为斜面,因此可把平抛运动沿斜面和垂直斜面方向的分解为:沿斜面向下初速度为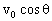 、加速度为
、加速度为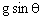 的匀加速直线运动及垂直斜面方向初速度为
的匀加速直线运动及垂直斜面方向初速度为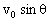 、加速度为
、加速度为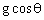 的匀减速直线运动.当小球在垂直斜面方向的速度减为零时,小球距斜面的距离最大,此过程的时间为
的匀减速直线运动.当小球在垂直斜面方向的速度减为零时,小球距斜面的距离最大,此过程的时间为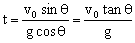 ,此时小球速度沿斜面向下,
,此时小球速度沿斜面向下,
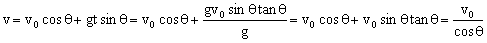 .
.
点评:本题也可以沿水平方向和竖直方向分解,求出两个分位移,再把两个分位移沿斜面和垂直斜面方向分解,求出垂直斜面方向上的两个分量之和,得出位移与时间的函数式,用求极值的方法,得出对应的时间。
解法三:
经过t时间时,水平分位移为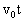 ,竖直分位移为
,竖直分位移为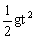 ,把两个分位移沿斜面和垂直斜面方向分解,设垂直斜面方向上的两个分量之和为
,把两个分位移沿斜面和垂直斜面方向分解,设垂直斜面方向上的两个分量之和为
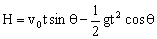
当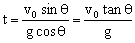 时,H最大值为
时,H最大值为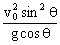 ,再求出竖直分速度
,再求出竖直分速度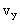 ,然后利用速度的合成得出此时小球的速度
,然后利用速度的合成得出此时小球的速度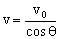 。
。
点评:此法运算量较大,但很容易得出一个“副产品”——最大距离H.若用上述两法求最大距离H,非常繁琐,不再赘述了.
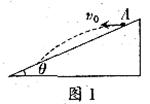
例2、如图3所示,在水平地面上固定一倾角θ=37°、表面光滑的斜面体,物体A以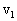 =6m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出。如果当A上滑到最高点时恰好被B物体击中.(A、B均可看作质点,sin37°=0.6,cos37°=0.8,g取10m/s2)求:
=6m/s的初速度沿斜面上滑,同时在物体A的正上方,有一物体B以某一初速度水平抛出。如果当A上滑到最高点时恰好被B物体击中.(A、B均可看作质点,sin37°=0.6,cos37°=0.8,g取10m/s2)求:
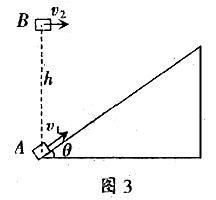
(1)物体B抛出时的初速度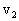 ;
;
(2)物体A、B间初始位置的高度差h.
解析:
(1)当A上滑到最高点时恰好被B物体击中,由运动的独立性原理,平抛物体B在水平方向的速度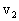 应等于A在水平方向上的平均速度
应等于A在水平方向上的平均速度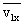 .
.
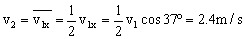
(2)物体A上滑过程中,由牛顿第二定律得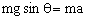
代入数据得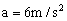
设经过t时间相撞,由运动学公式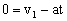 代入数据得t=1s,物体A、B间的高度差
代入数据得t=1s,物体A、B间的高度差