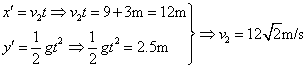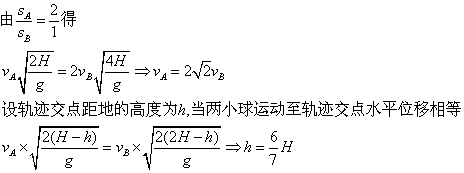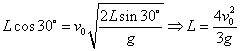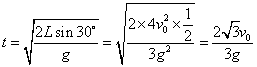| 平抛运动应用(二) |
主编:黄冈中学物理集体备课组
例1、如图所示,排球场地长为18m,设球网高度为2m,运动员站在离网3m的线上(图中用虚线表示)正对网前跳起将球水平击出(空气阻力不计).
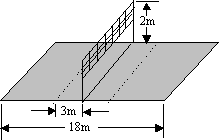
(1)设击球点在3m线正上方2.5m处,试问击球的速度在什么范围内才能使球既不能触网也不越界?
(2)若击球点在3m线正上方小于某一个值,那么无论以多大速度击球,球不是触网就是越界.试求这个高度.
解:
若击球水平速度过小,球可能触网;若击球水平速度过大,球可能越界.
(1)若刚好不触网,设击球速度为v1,则水平位移为3m的过程中,
水平方向:x=v1t
v1t=3 ①
竖直方向:
②
由①②得:
同理刚好不越界,设击球速度为v2,则
则球既不能触网也不越界的速度满足
(2)设击球高度为H时,击出的球刚好触网或落在边界线上.
刚好不触网时:v0t1=3 ③
④
此时也刚好到达边界:v0t2=12 ⑤
⑥
由③④⑤⑥得:H=2.13m
即当击球高度小于2.13时,无论水平速度多大,球不是触网就是越界.
例2、从高为H的A点平抛一物体,其水平射程为2s,在A点正上方距地面高为2H的B点,向同一方向平抛另一物体,其水平射程为s.两物体轨迹在同一竖直平面内且都恰好从同一屏的顶端擦过,求屏的高度.
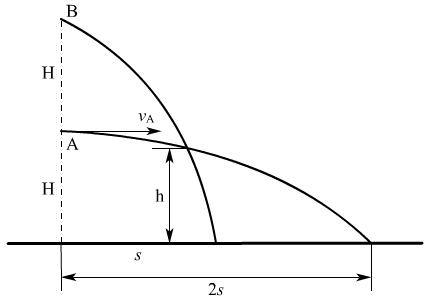
解:
例3、如图示,AB为斜面,倾角为30°,小球从A点以初速度v0水平抛出,恰好落到B点.求:
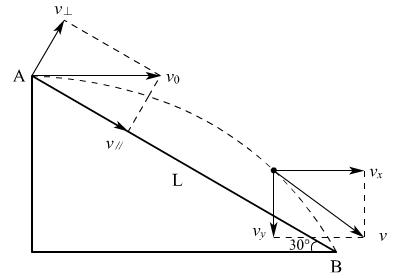
(1)AB间的距离;
(2)物体在空中飞行的时间;
(3)从抛出开始经多少时间小球与斜面间距离最大?
解:
(1)水平位移:
(2)物体在空中飞行时间
(3)当小球作平抛运动轨迹上某一点速度与斜面平行时,该点离斜面距离最远.
方法①:
方法②:由分运动的独立性,把平抛运动分解成垂直斜面方向的分运动和平行于斜面方向的分运动的合运动.
v⊥=v0sin30°=
a⊥=gcos30°=
垂直斜面作初速为
,加速度为
的匀减速直线运动
平行于斜面作v11=v0cos30°=
,a11=gcos60°=
的匀加速直线运动
当在垂直斜面方向速度减为0时距斜面最远:
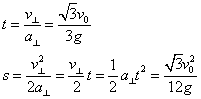
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -