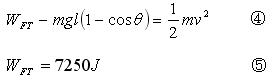例1、有一种叫“飞椅”的游乐项目,示意图如图所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ,不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.
解析:
设转盘转动角速度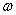 时,夹角θ夹角θ
时,夹角θ夹角θ
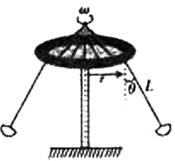
座椅到中心轴的距离: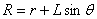 ①
①
对座椅分析有: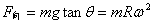 ②
②
联立两式得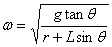
例2、如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′转动,筒内壁粗糙,筒口半径和筒高分别为R和H,筒内壁A点的高度为筒高的一半,内壁上有一质量为m的小物块,求:
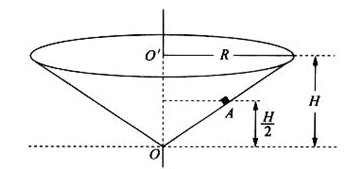
①当筒不转动时,物块静止在筒壁A点受到的摩擦力和支持力的大小;
②当物块在A点随筒做匀速转动,且其所受到的摩擦力为零时,筒转动的角速度.
解析:
①由平衡条件可知,
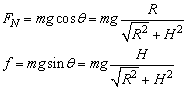
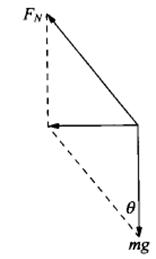
②物块受力如图,由F=mg知
例3、“旋转飞椅”(FLYING CHAIR)是公园中常见的大型游乐设施,通常其高度达10m以上,占地面积超过300m2,一般装有24只飞椅可同时乘座24人,在380V、7.5KW的电机驱动下,可在0~8.5r/min的转速下旋转。当飞椅稳定转动后,飞椅在距地面一定高度的水平面内做匀速圆周运动。
“旋转飞椅”可简化成这样的模型:
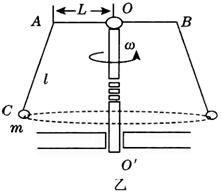
如图(乙)所示,AB为与竖直转轴OO′固定的水平横梁,长度为2L,AC是悬挂飞椅的绳索,飞椅拴在绳索的末端C处,设施静止时,绳索AC竖直。游戏开始时,人乘座在飞椅中,闭合电源开关,电机带动OO′轴开始转动,飞椅在绳的牵引下开始加速。随着转速的增加,飞椅(连同人)的高度逐渐上升,与OO′的距离逐渐增大,当设施转动稳定后,飞椅(连同人)在水平面内做匀速圆周运动。已知L=8m,AC长l=10m,飞椅(连同人,可视为质点)的总质量为m=100kg,设施稳定转动时绳索AC的拉力为1250N,不考虑绳索质量和空气阻力,取g=l0m/s2,求:
(1)设施转动稳定后,飞椅(连同人)在水平面内做匀速圆周运动的线速度大小。
(2)从闭合电源到设施转动稳定的过程中,绳索对飞椅(连同人)做的功。

解:
(1)当飞椅稳定后
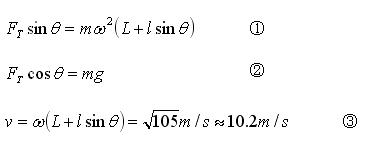
(2)从飞椅开始转动到稳定的过程中