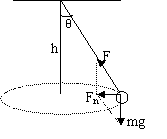
1.向心力和向心加速度:
设摆球的质量为m,摆线长为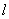 ,与竖直方向的夹角为θ,摆球的线速度为
,与竖直方向的夹角为θ,摆球的线速度为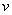 ,角速度为
,角速度为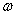 ,周期为T,频率为
,周期为T,频率为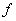 。
。
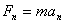 ,
,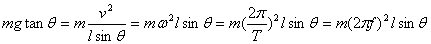 ,
,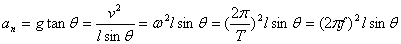
2.摆线的拉力:
有两种基本思路:当θ角已知时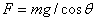 ,当θ角未知时
,当θ角未知时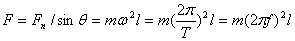
3.周期的计算:
设悬点到圆周运动圆心的距离为h,根据向心力公式有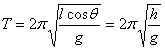 ,由此可知高度相同的圆锥摆,周期相同,与
,由此可知高度相同的圆锥摆,周期相同,与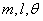 无关。
无关。
4.动态分析:当角速度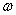 增大时,根据
增大时,根据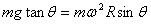 有
有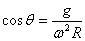 ,
,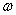 增大,
增大, 增大,向心力增大,回旋半径增大,周期变小。
增大,向心力增大,回旋半径增大,周期变小。
例1、将一个半径为R的内壁光滑的半球形碗固定在水平地面上,若使质量为m的小球贴着碗的内壁在水平面内以角速度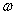 做匀速圆周运动,如图,求圆周平面距碗底的高度。若角速度
做匀速圆周运动,如图,求圆周平面距碗底的高度。若角速度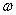 增大,则高度、回旋半径、向心力如何变化?
增大,则高度、回旋半径、向心力如何变化?
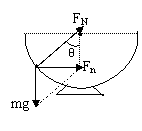
解析:
本题属于圆锥摆模型,球面的弹力类比于绳的拉力,球面半径类比于绳长。 ,故
,故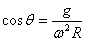 ,圆周平面距碗底的高度为
,圆周平面距碗底的高度为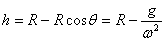 。若角速度
。若角速度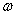 增大,则有θ增大,高度h变大,回旋半径变大,向心力变大。
增大,则有θ增大,高度h变大,回旋半径变大,向心力变大。
点评:本题形式上不属于圆锥摆模型,但实质即为圆锥摆模型。
例2、一个内壁光滑的圆锥筒绕其竖直轴线以角速度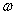 做匀速转动,在圆锥筒内壁的A处有一质量为m的小球与圆锥筒保持相对静止,在水平面内做匀速圆周运动,如图,当圆锥筒的角速度增大时,则小球到锥底的高度,回旋半径,向心力分别如何变化?
做匀速转动,在圆锥筒内壁的A处有一质量为m的小球与圆锥筒保持相对静止,在水平面内做匀速圆周运动,如图,当圆锥筒的角速度增大时,则小球到锥底的高度,回旋半径,向心力分别如何变化?
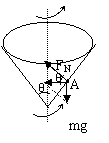
解析:
小球受两个力mg、FN,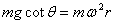 ,角速度增大时,由于角度不变,故向心力不变,回旋半径r减小,小球到锥底的高度降低。
,角速度增大时,由于角度不变,故向心力不变,回旋半径r减小,小球到锥底的高度降低。
点评:本题区别于例1,不属于圆锥摆模型。圆锥摆模型是当角速度发生变化时,圆锥摆顶点保持不变,即摆长不变。本题动态分析的结论和例1相反。
例3、一光滑的圆锥体固定在水平桌面上,其轴线沿竖直方向,其顶角为600,如图所示,一条长为L的轻绳,一端固定在锥顶O点,另一端拴一质量为m的小球,小球的速率v绕圆锥的轴线做水平面内的匀速圆周运动,求:(1)当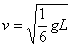 ,绳上的拉力多大?(2)当
,绳上的拉力多大?(2)当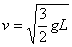 ,绳上的拉力多大?
,绳上的拉力多大?
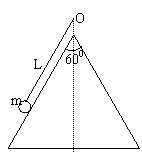
解析:
当圆锥体刚好对斜面没有压力时,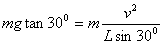 ,求得小球的线速度为
,求得小球的线速度为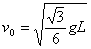 。(1)当
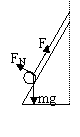
。(1)当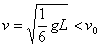 小球不做圆锥摆运动,小球受三个力,如图示,用正交分解法解题,在竖直方向
小球不做圆锥摆运动,小球受三个力,如图示,用正交分解法解题,在竖直方向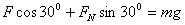
 ,在水平方向
,在水平方向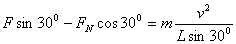 ,解得
,解得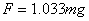 。(2)当
。(2)当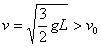 ,小球做圆锥摆运动,且
,小球做圆锥摆运动,且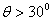 ,设此时绳与竖直方向的夹角为
,设此时绳与竖直方向的夹角为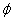 ,则有
,则有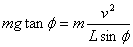 ,解得
,解得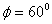 ,因此
,因此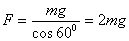 。
。
点评:本题要先判断究竟物体是否属于圆锥摆模型。判断时,先根据临界问题,当圆锥体刚好对斜面没有压力时,求得小球的线速度为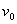 。当
。当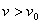 时,小球做圆锥摆运动,
时,小球做圆锥摆运动,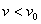 时,小球不做圆锥摆运动。
时,小球不做圆锥摆运动。