| 命题及其关系 |
主编:黄冈中学数学集体备课组
正确使用逻辑用语和逻辑关系是现代社会公民应该具备的基本素质.逻辑是研究思维形式和规律的科学,“数学是思维的科学”,逻辑与数学有着天然的联系.
本章我们将从命题及其关系入手,学习四种命题的相互关系、充分条件和必要条件,学习逻辑用语,了解数理逻辑的有关知识,体会逻辑用语在表述或论证中的作用,使以后的论证和表述更加准确、清楚和简洁.在学习过程中我们应避免对逻辑用语的机械记忆和抽象解释,而应该通过具体、生动的实例来使学生体会常用的逻辑用语,学习使用常用的逻辑用语,掌握常用逻辑用语,并在使用过程中纠正出现的逻辑错误.
思考1:下列语句的表述形式有什么特点?你能判断他们的真假吗?
(1)若直线a∥b,则直线a与直线b没有公共点.
(2)2+4=7.
(3)垂直于同一条直线的两个平面平行.
(4)若x2=1,则x=1.
(5)两个全等三角形的面积相等.
(6)3能被2整除.
答案:(1)(3)(5)的判断为真,(2)(4)(6)的判断为假.
1、定义:一般地,我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.
命题的定义的要点:能判断真假的陈述句.
例1、判断下列语句是否为命题?
(1)空集是任何集合的子集;
(2)若整数a是素数,则a是奇数;
(3)指数函数是增函数吗?
(4)若平面上两条直线不相交,则这两条直线平行;
(5)
=-2;
(6)x>15;
(7)请你把那本书递给我;
(8)今天天气真好啊!
答案:(1)(2)(4)(5)是命题;(3)(6)(7)(8)不是命题.
总结:
判断一个语句是不是命题,关键看两点:第一是“陈述句”,第二是“可以判断真假”,这两个条件缺一不可.疑问句、祈使句、感叹句均不是命题.
2、命题的构成——条件和结论
定义:从构成来看,所有的命题都由条件和结论两部分构成.在数学中,命题常写成“若p,则q”或者“如果p,那么q”这种形式,通常,我们把这种形式的命题中的p叫做命题的条件,q叫做命题的结论.
例2、指出下列命题中的条件p和结论q,并判断各命题的真假.
(1)若整数a能被2整除,则a是偶数.
(2)若四边形是菱形,则它的对角线互相垂直平分.
(3)若a>0,b>0,则a+b<0.
答案:
(1)条件p:整数a能被2整除,结论q:a是偶数.(真)
(2)条件p:四边形是菱形,结论q:它的对角线互相垂直平分.(真)
(3)条件p:a>0,b>0,结论q:a+b<0.(假)
3、命题的分类——真命题、假命题的定义.
真命题:如果由命题的条件p通过推理一定可以得出命题的结论q,那么这样的命题叫做真命题.
假命题:如果由命题的条件p通过推理不一定可以得出命题的结论q,那么这样的命题叫做假命题.
说明:
(1)注意命题与假命题的区别.如:“作直线AB”.这本身不是命题.也更不是假命题.
(2)命题是一个判断,判断的结果就有对错之分.因此强调真假命题的大前提,首先是命题.
例3、把下列命题写成“若p,则q”的形式,并判断是真命题还是假命题:
(1)面积相等的两个三角形全等;
(2)负数的立方是负数;
(3)对顶角相等;
(4)垂直于同一条直线的两个平面平行.
答案:
(1)若两个三角形的面积相等,则这两个三角形全等;(假命题)
(2)若一个数是负数,则它的立方是负数;(或者若一个数是负数的立方,则它是负数)(真命题)
(3)若两个角是对顶角,则它们相等;(真命题)
(4)若两个平面垂直于同一条直线,则它们平行.(真命题)
思考2:判断下列命题的真假,你能发现各命题之间有什么关系?
①如果两个三角形全等,那么它们的面积相等;
②如果两个三角形的面积相等,那么它们全等;
③如果两个三角形不全等,那么它们的面积不相等;
④如果两个三角形的面积不相等,那么它们不全等.
答案:
命题①④为真,②③为假;
①与②、③与④条件和结论互逆,①与③、②与④条件和结论互否.
4、原命题与逆命题
在两个命题中,如果第一个命题的条件(或题设)是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题;如果把其中一个命题叫做原命题,那么另一个叫做原命题的逆命题.
例如上面思考中的①与②,③与④.
5、原命题与否命题
在两个命题中,一个命题的条件和结论分别是另一个命题的条件的否定和结论的否定,这样的两个命题就叫做互否命题,若把其中一个命题叫做原命题,则另一个就叫做原命题的否命题.
例如上面思考中的①与③,②与④.
6、原命题与逆否命题
在两个命题中,一个命题的条件和结论分别是另一个命题的结论的否定和条件的否定,这样的两个命题就叫做互为逆否命题,若把其中一个命题叫做原命题,则另一个就叫做原命题的逆否命题.
例如上面思考中的①与④,②与③.
概括地说,设命题⑴为原命题,则命题⑵为逆命题;命题⑶为否命题;命题⑷为逆否命题.
总结:关于逆命题、否命题与逆否命题,也可以这样表述:
(1)交换原命题的条件和结论,所得的命题是逆命题;
(2)同时否定原命题的条件和结论,所得的命题是否命题;
(3)交换原命题的条件和结论,并且同时否定,所得的命题是逆否命题.
7、四种命题的形式
一般的,我们用p和q分别表示原命题的条件和结论,用┐p和┐q分别表示p和q的否定,于是四种命题的形式就是:
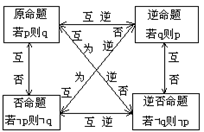
原命题:若p则q;
逆命题:若q则p;
否命题:若┐p则┐q;
逆否命题:若┐q则┐p.
例4、写出命题“若a=0,则ab=0”的逆命题、否命题、逆否命题,并判断各命题的真假.
解:
原命题:若a=0,则ab=0是真命题;
逆命题:若ab=0,则a=0是假命题;
否命题:若a
0,则ab
0是假命题;(备注:视频中的引号删去)
逆否命题:若ab
0,则a
0是真命题.(备注:视频中的引号删去)
例5、把下列命题改写成“若p则q”的形式,并写出它们的逆命题、否命题与逆否命题,同时指出它们的真假.
(1)两个全等的三角形的三边对应相等;
(2)四边相等的四边形是正方形;
(3)负数的平方是正数.
解:
(1)原命题可以写成:若两个三角形全等,则这两个三角形的三边对应相等;(真)
逆命题:若两个三角形的三边对应相等,则这两个三角形全等;(真)
否命题:若两个三角形不全等,则这两个三角形不是三边对应相等;(真)
逆否命题:若两个三角形不是三边对应相等,则这两个三角形不全等;(真)
(2)原命题可以写成:若一个四边形四边相等,则它是正方形;(假)
逆命题:若一个四边形是正方形,则它的四条边相等;(真)
否命题:若一个四边形四边不相等,则它不是正方形;(真)
逆否命题:若一个四边形不是正方形,则它的四条边不相等;(假)
(3)原命题可以写成:若一个数是负数,则它的平方是正数;(真)
逆命题:若一个数的平方是正数,则它是负数;(假)
否命题:若一个数不是负数,则它的平方不是正数;(假)
逆否命题:若一个数的平方不是正数,则它不是负数.(真)
归纳:原命题为假,它的逆命题、否命题不一定为假;原命题为假,它的逆否命题一定为假.
8、四种命题的真假性之间的关系如下:
结论一:原命题与它的逆否命题同真假;
结论二:两个命题为互逆命题或互否命题,它们的真假性没有关系.
例6、证明:若
,则
.
证明:
原命题的逆否命题为:若x、y中至少有一个不为0,则
.
不妨设
,则
,而
,所以
,
∴原命题的逆否命题为真命题,
所以原命题为真命题,即所求证成立.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -