| 抛物线及其标准方程 |
主编:黄冈中学数学集体备课组
1、抛物线的定义:
平面内与一个定点F和一条定直线l(不过该定点)的距离相等的点的轨迹叫抛物线;
点F叫抛物线的焦点,直线l叫做抛物线的准线.
2、抛物线的标准方程:
①推导过程:
如图,建立直角坐标系xOy,使x轴经过点F且垂直于直线l,垂足为K,并使原点与线段KF的中点重合.
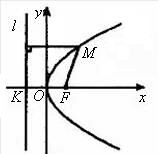
设|KF|=p (p>0),那么焦点F的坐标为(
,准线l的方程为
设点M(x,y)是抛物线上任意一点,点M到l的距离为d.
由抛物线的定义,抛物线就是集合
将上式两边平方并化简,得y2=2px ①
方程y2=2px叫抛物线的标准方程,它表示的抛物线的焦点在x轴的正半轴上,坐标是
它的准线方程是
②抛物线标准方程的四种形式:
一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其他几种形式:y2=-2px,x2=2py,x2=-2py.这四种抛物线的图形,标准方程,焦点坐标及准线方程列表如下:
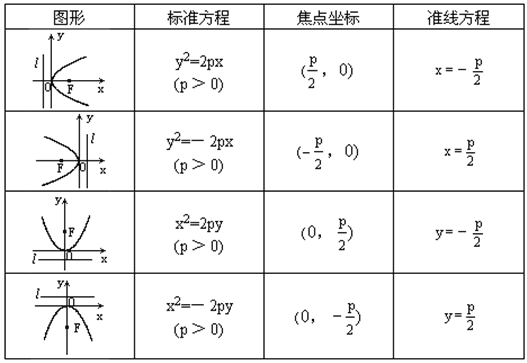
相同点:(1)顶点为原点;(2)对称轴为坐标轴;(3)顶点到焦点的距离=顶点到准线的距离=
.
不同点:(1)一次变量为
,则对称轴为
轴;
(2)一次项的系数为正(负),则开口向坐标轴的正(负)方向.
例1、已知抛物线方程如下,求出焦点坐标和准线方程.
(1)
(2)
(3)
(
)
解:
(1)易知
,焦点F
,准线方程是
.
(2)
化成
,∴
,焦点F
,准线方程是
.
(3)
化成
,∴
,焦点F
,准线方程是
.
例2、求适合下列条件的抛物线的标准方程:
(1)过点(-3,2);
解:
设抛物线方程为x2=2p1y或y2=-2p2x(p1>0,p2>0),
代入点(-3,2)得:9=4p1或4=-2p2·(-3).
解得
.
故抛物线的标准方程为
(2)焦点在直线x-2y-4=0上.
解:
直线x-2y-4=0与坐标轴的交点为(4,0),(0,-2).
①当焦点为(4,0)时,抛物线设为y2=2p1x(p1>0),
.
∴抛物线为y2=16x.
②当焦点为(0,-2)时,抛物线设为x2=-2p2y(p2>0),
.
∴抛物线为x2=-8y.
∴抛物线的方程为y2=16x或x2=-8y.
例3、点M与点
的距离比它到直线l:
的距离小1,求点M的轨迹方程.
解:
题意等价于点M到点
的距离与到直线
的距离相等,
∴M的轨迹为以
为焦点,
为准线的抛物线,所求的方程为
.
例4、动点M到y轴的距离比到点(2,0)的距离小2,求点M的轨迹方程.
解:
题目条件等价于动点M到x=-2的距离等于到点(2,0)(备注:视频中-2改为2)的距离,或M在x轴的非正半轴上,∴轨迹方程为y2=8x或y=0(x≤0).
例5、已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求出取最小值时P点坐标.
解:
当x=3时,y2=2×3=6,∴
.
,∴A在抛物线内部.
抛物线y2=2x,焦点为
,准线为L:
.
过P作
,
为垂足,则
.
,当PA,
共线时,
取到最小值
.
此时P的纵坐标为2,∴横坐标为2.∴P为(2,2).
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -