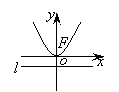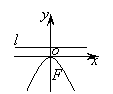| 抛物线的简单几何性质 |
主编:黄冈中学数学集体备课组
我们根据抛物线的
标准方程:
(p>0)来研究它的简单几何性质.
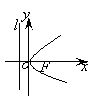
1、范围
因为p>0,由方
程可知x≥0 ,所以抛物线在y轴的右侧,当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
2、对
称性
以-y代y,方程不变,所以抛物线关于x轴对称.我们把抛物线的对称轴叫做抛物线的轴.
3、顶点
抛物线与它的轴的交点叫做抛物线的顶点,在方程中,当y=0 时x=0 ,因此抛物线的顶点就是坐标原
点.
4、离心率
抛物线上的点到焦点的距离和它到准线的距离的比,叫做抛物线的离心率,由抛物线的定义可知e=1.
抛物线的4种形式的标准方程图形的简单几何性质可以得到如下的表格:
标准方程
图形
焦点坐标
准线方程
范围
x≥0
x≤0
y≥0
y≤0
对称性
轴
轴
轴
轴
顶点
离心率
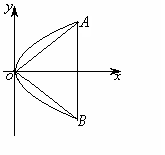
例1、正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线
上,求这个正三角形的边长.
解:
△OAB的顶点A、B在y2=2px上,且设点
,
,
则
,
,又
,
所以
,
,
即
,
∴
.
∵
,
,
,∴
,∴
.
∴AB关于x轴对称.
∴
,∴
.
又
,解得
,∴边长等于
.
例2、斜率为1的直线经过抛物线
的焦点,与抛物线相交于两点A、B,求线段AB的长度.
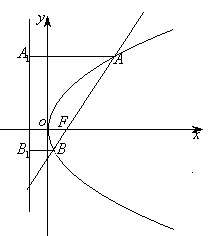
解:
的焦点为F(1,0),∴AB方程为y=x-1.
,
.
设
.
.
(法二)由抛物线的焦点弦长公式:
.
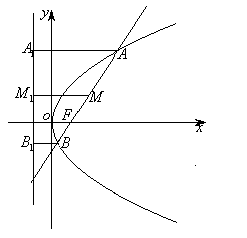
说明:抛物线的焦点弦常见的结论.
焦点弦:过
的焦点弦
,记
,
,
(1)弦长
(
为弦的倾斜角);
(2)
两点坐标之间的关系:
,
;
(3)
(M为AB的中点);
(4)以AB为直径的圆与准线相切;
(5)当弦
轴时,焦点弦AB长度最短.
例3、A、B是抛物线
上的两点,满足
(O为坐标原点).
(1)求证:A、B两点的横坐标之积为定值;
(2)直线AB经过一定点.
解:
(1)设
,设OA的方程为y=kx(k≠0),则OB的方程为
,
由
,∴
,同理得
.
∴
(定值),且
(定值).
∴A、B两点的横坐标之积为定值.
(2)由(1)知当
时,AB直线所在斜率
,
∴AB所在直线方程:
,即
,
该直线恒过点
.
当
或
时,直线AB方程为
,直线AB也经过定点
.
∴直线AB一定经过定点(2p,0).
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -