6、
解析:(一)几何法:如图,令|AF|=x,则|AA1|=x;|FB|=y,则|BB1|=y
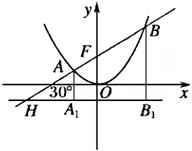
∴|HB|=2y,∴|HB|=2x+x+y=2y,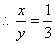
(二)特殊值法:令p=2,则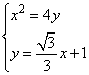 ,求出A、B坐标即可. ,求出A、B坐标即可.
7、2
解析:由抛物线定义知P到准线l2:x=-1的距离等于它到焦点(1,0)的距离,所以P到直线l1和l2的距离之和最小值等于焦点到l1的距离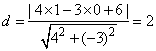 . .
8、6
解析:由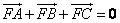 知F为△ABC的重心, 知F为△ABC的重心,
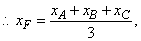 即xA+xB+xC=3, 即xA+xB+xC=3,
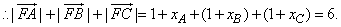
9、y=x
解析:由题意知抛物线方程为y2=4x,直线过点(2,2),且斜率存在,
所以设直线方程为:y=k(x-2)+2,联立方程消x得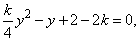
设A(x1,y1),B(x2,y2),得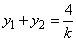 , ,
又由已知y1+y2=4,得k=1,所以直线方程为y=x. |