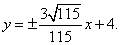例、(浙江卷)已知抛物线C1:x2=y,圆C2: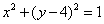 的圆心为点M.
的圆心为点M.
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.
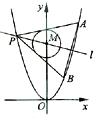
解析:
(1)由题意可知,抛物线C1的准线方程为
所以圆心M(0,4)到准线的距离是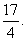
(2)设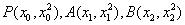 ,
,
则题意得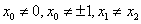 ,
,
设过点P的圆C2的切线方程为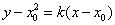 ,
,
即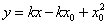 ①
①
则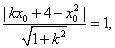
即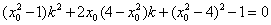 ,
,
设PA,PB的斜率为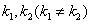 ,则
,则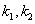 是上述方程的两根,所以
是上述方程的两根,所以
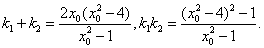
将①代入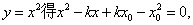
由于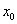 是此方程的根,
是此方程的根,
故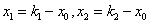 ,所以
,所以
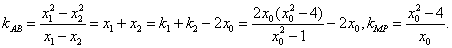
由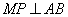 ,得
,得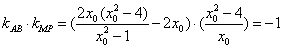 ,
,
解得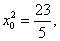
即点P的坐标为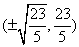 ,
,
所以直线l的方程为