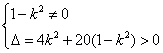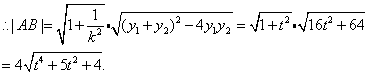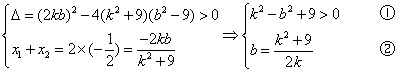| 直线和圆锥曲线 |
主编:黄冈中学数学集体备课组
1、直线与圆锥曲线的位置关系
直线与圆锥曲线的位置关系,从几何角度可分为三类:无公共点,仅有一个公共点及有两个相异公共点.
直线与圆锥曲线的位置关系的研究方法可通过代数方法即解方程组的办法来研究.因为方程组解的个数与交点的个数是一样的.
直线与圆锥曲线的位置关系可分为:相交、相切、相离.这三种位置关系的判定条件可归纳为:
设直线
:
,圆锥曲线
,由
,
消去y(也可以消去x)得:
,
,
当
时,△>0
相交
两个公共点;
△=0
相切
一个公共点;
△<0
相离
没有公共点.
注意:直线与抛物线、双曲线有一个公共点是直线与抛物线、双曲线相切的必要条件,但不是充分条件.
对于抛物线来说,平行于对称轴的直线与抛物线相交于一点,但并不是相切;对于双曲线来说,平行于渐近线的直线与双曲线只有一个交点,但并不相切.
2、直线和圆锥曲线相交的弦长公式
设直线l:
,圆锥曲线:
,它们的交点为A (x1,y1),B(x2,y2),
且由
,消去y得
,
,
则弦长公式为:
|AB|=
=
=
.
将直线方程
:
代入曲线方程整理后得到关于y的一元二次方程,其弦长公式为
.
3、中点弦问题
①设直线方程为y=kx+m,代入到圆锥曲线方程之中,消元后得到一元二次方程,再利用根与系数的关系去处理(由于直线方程与圆锥曲线方程均未定,因而通常计算量较大);
②利用点差法:设A(x1,y1),B(x2,y2)是椭圆
上不同的两点,且x1≠x2,x1+x2≠0,M(x0,y0)为AB的中点,则
两式相减可得
.
即可得到直线的斜率k与弦的中点之间的关系:
,对于双曲线、抛物线,可得类似的结论.
例1、如果直线l:
与双曲线
,试分别确定下列条件下的k的范围,
(1)直线l与双曲线没有交点;
(2)直线和双曲线有且仅有一个交点;
(3)直线和双曲线有两个不同的交点,若与双曲线右支有两个不同的交点呢?
解:
由
得
,
(1)若直线
与双曲线没有交点,则
且
,解得
或
.
(2)若直线和双曲线有且仅有一个交点,则
或
,
解得
或
.
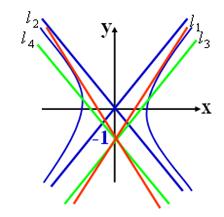
(3)若直线和双曲线有两个不同的交点,则
解得
且
.
若与双曲线右支有两个不同的交点,则
,解得
.
例2、已知抛物线
,过点
的直线l与抛物线交于A,B两点,求线段AB的最短长度及此时对应的直线方程.
解:
依题意可以设直线
的方程为
,
代入抛物线
得:
,
.
设
,所以
,
,
易知在
时,
,
此时l的方程为x=4.
例3、已知椭圆方程为
,一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为-
,求直线l倾斜角的取值范围.
解:
设直线l的方程为y=kx+b(k≠0).
代入椭圆方程中得
,设
.
∴有
将②代入①化简后,得
,解得
(舍负),
∴
.
∴倾斜角范围为
.
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -