| 空间向量及其加、减、数乘运算 |
主编:黄冈中学数学集体备课组
一、空间向量的相关概念:
空间向量:在空间,我们把具有大小和方向的量叫做向量;
向量的模(或长度):空间向量的大小;
零向量:长度为零的向量;
单位向量:模为1 的向量;
相反向量:长度相等而方向相反的两个向量互为相反向量;
相等向量:方向相同且模相等的向量;
空间的两个向量都是共面向量:空间的任意两个向量都可以平移到同一个平面内,成为同一平面的两个向量.
说明:(1)由于空间任意两个向量都可转化为共面向量,所以凡涉及空间两个向量的问题,平面向量中的有关结论仍适用.
(2)空间向量a、b确定的平面不是一个,而是一个互相平行的平面的集合,但研究解决问题时,一般只要在其中一个平面内考虑即可.
二、空间向量的加法、减法运算
空间向量的加法:符合平行四边形法则或三角形法则(异起点,首尾连)如:
.
空间向量的减法:符合三角形法则(共起点,指被减)如:
.
加法的运算性质:(1)加法交换律:
;
(2)加法结合律:
.
三、空间向量的数乘运算
与平面向量一样,实数
与空间向量
的乘积
仍然是一个向量,叫做向量的数乘运算.
的长度为
;当
时,
与
同向,当
时,
与
反向,当
时,
.
空间向量的数乘运算的性质:
(1)数乘分配律:
;
(2)结合律:
.
四、空间共线向量
1、定义:表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量.
平行于
记作
.
2、共线向量定理:空间任意两个向量
、
(
),
的充要条件是存在实数λ,使
=λ
.
3、推论:如果
为经过已知点A且平行于已知非零向量
的直线,那么对于任意一点O,点P在直线
上的充要条件是存在实数t满足等式 :
.
其中向量
叫做直线
的方向向量.
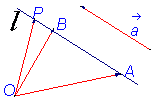
4、结论:用向量证明P与A、B共线的方法:
证明等式
或
或
或
成立.
五、空间共面向量
1、定义:平行于同一平面的向量,叫做共面向量.
2、共面向量定理:如果两个向量
不共线,
与向量
共面的充要条件是:
存在有序实数对
使
.
3、推论:空间一点P位于平面MAB内的充分必要条件是
存在有序实数对
,使
①
或对空间任一点
,有
②
或
③
上面①式叫做平面MAB的向量表达式.
例1.如图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算的结果为向量
的共有( )
①
; ②
;
③
; ④
.
A.1个 B.2个 C.3个 D.4个
答案:D
例2.在如图四面体ABCD中,
,M为BC的中点,Q为
的重心,试用
表示向量
.
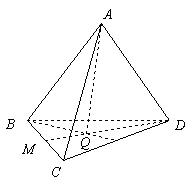
解:因为M为BC的中点,所以
.
.
例3.已知E、F、G、H分别是空间四边形ABCD边AB、BC、CD、DA的中点.
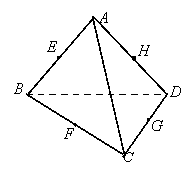
(1)用向量法证明E、F、G、H四点共面;
(2)用向量法证明BD//平面EFGH;
(3)设M是EG和FH的交点,求证:对空间任一点O,有
.
(1)证明:可转化为证明G在由E、F、H确定的平面上.
∴G在由E、F、H确定的平面上,即所求证成立.
(2)证明:
,∴BD//EH.
(3)证明:由(2)中知:
,
,
∴四边形
为平行四边形.
∴M是EG、FH的中点,
∴
.
即所求证成立.
例4.已知O是空间任一点,A、B、C、D四点满足任三点均不共线,但四点共面,且
,则
_____________.
解:
将等式
转化为从
点出发的向量等式得:
,
由结论知
,
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -