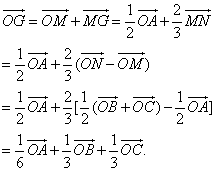| 空间向量的坐标表示及坐标运算 |
主编:黄冈中学数学集体备课组
一、空间向量基本定理
如果三个向量a、b、c不共面,那么对于空间任一向量p,存在一个唯一的有序实数组x、y、z,使:p=xa+yb+zc.
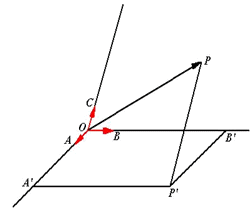
证明:
存在性:任取点O,作
,
,
过点P作
交平面OAB于点
,在平面OAB内过
分别作OA、OB的平行线交OB、OA交于点
、
,
由向量共线知:
,
,
,
所以
.
唯一性:设另有一组实数
,使得
,则有
,∴
.
∵
不共面,∴
,即
.
故实数x、y、z是唯一的.
由上述定理可知,空间任一向量均可以由空间不共面的三个向量生成,我们把{a、b、c}叫做空间的一个基底,a、b、c都叫做基向量.
说明:①空间任意三个不共面的向量都可以构成空间的一个基底.
②三个向量不共面就隐含着它们都不是零向量(零向量与任意非零向量共线,与任意两个非零向量共面).
③一个基底是不共面的三个向量构成的一个向量组,一个基向量是指基底中的某一个向量.
二、单位正交基底和空间直角坐标系
单位正交基底:如果空间的一个基底的三个向量互相垂直,且长度都为1,则这个基底叫做单位正交基底,常用
表示.
空间直角坐标系:在空间选定一点O和一个单位正交基底
,以点O为原点,分别以
为正方向建立三条数轴:x轴、y轴、z轴,则建立了一个空间直角坐标系
,点O叫原点,向量
都叫坐标向量.
三、空间向量的坐标
给定空间直角坐标系和向量
,设
为坐标向量,则存在唯一的有序实数组
,使
,有序实数组
叫作向量
在空间直角坐标系
中的坐标,记作
.
四、空间向量的直角坐标运算:
若
,
,则
(1)
;
(2)
;
(3)
,
(4)
;
(5)
.
(6)若
,
,则
.
(7)向量的模为:
,这个式子我们称为向量的长度公式.
(8)空间向量的夹角公式:
.
五、空间两点间的距离公式与中点坐标公式:
已知点
,
,则
,AB的中点坐标为
.
例1、已知空间四边形OABC,其对角线OB,AC,M,N分别是对边OA,BC的中点,点G在线段MN上,且MG=2GN,用基底向量
表示向量
、
.
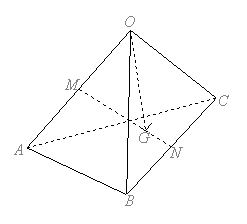
解:
.
例2、已知
,
,求
,
,
,
,
.
解:
.
.
.
.
或
.
.
.
或
.
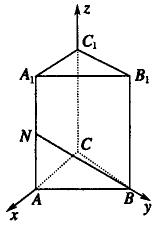
例3、如图,在直三棱柱ABC-A1B1C1中,AC=BC=1,AA1=2,∠ACB=90°.
(1)若点N是AA1的中点,求点B与N的距离;
(2)求向量
夹角的余弦.
解:
以C为原点,以
的方向为x轴、y轴、z轴的正方向,建立空间直角坐标系C-xyz.
(1)依题意得B(0,1,0),N(1,0,1),
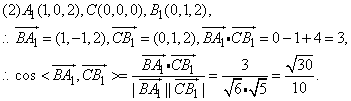
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -