例、已知：a2＋b2＋c2＝1，x2＋y2＋z2＝1，其中a，b，c，x，y，z均为实数，求证：－1≤ax＋by＋cz≤1．
分析：
a2＋b2＋c2＝1，即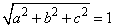
为向量的长度公式，而ax＋by＋cz可以理解为数量积．
证明：
构造向量α＝（a，b，c），β＝（x，y，z），
则由题设知，|α|2＝1，|β|2＝1，
∴|α|＝1，|β|＝1．
令α、β的夹角为θ，则θ∈[0，π]，
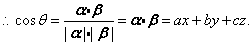
又∵－1≤cosθ≤1，∴－1≤ax＋by＋cz≤1．
点评：
这种方法证明不等式，要求学生对向量的坐标公式理解深刻，不易想到，不过方法简单，出奇制胜．
