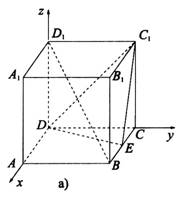
例、如图所示，在正方体ABCD－A1B1C1D1中，E为棱BC的中点．
(1)求证：BD1//平面C1DE；
(2)试在棱CC1上求一点P，使得平面A1B1P⊥平面C1DE．
解析：
（1）如图a所示，建立空间直角坐标系Dxyz，设正方体棱长为1，
则D（0，0，0），D1（0，0，1），E（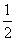
，1，0），B（1，1，0），C1（0，1，1），
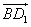=（－1，－1，1），
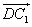=（0，1，1），
=（
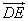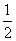，1，0）．
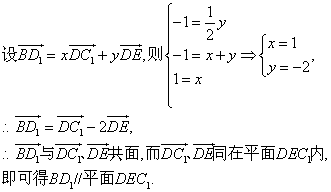
(2)易知A1B1⊥平面B1C，∴A1B1⊥C1E，要平面A1B1P⊥平面C1DE，只要C1E⊥平面A1B1P即可，则要C1E⊥B1P．
P在C1C上，设P的坐标为P(0，1，t)，则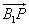
=(－1，0，t－1)．
．
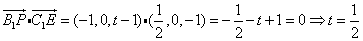即P(0，1，t)，∴P在CC1的中点时可使得平面A1B1P⊥平面C1DE．
