| 立体几何中的向量方法(2) —向量法求空间的角 |
主编:黄冈中学数学集体备课组
一、异面直线所成的角:
1.范围:
;
2.向量求法:设
分别是两条异面直线
的方向向量,则
所成角的余弦值为
.
(说明:要注意异面直线所成的角与向量夹角的区别与联系.)
二、直线与平面所成的角:
1.范围:
;
2.向量求法:设直线
是平面
的一条斜线,
是直线
的方向向量,
是
的法向量,
则
与
所成角的正弦值为
.
三、二面角:
1.范围:
2.向量求法:①设
分别是二面角
的两个面内与棱
垂直的向量,而二面角的大小是
或其补角的大小;
②设
分别是二面角
的两个面
的法向量,则二面角的平面角的大小就是
或其补角的大小.
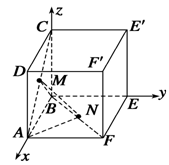
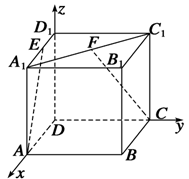
例1.正方体ABCD—A1B1C1D1中,E、F分别是A1D1、A1C1的中点.
(1)求异面直线AE与CF所成角的余弦值;
(2)求直线CF与平面ABE所成的角的正弦值.
解:
(1)如图建立空间直角坐标系D-xyz,设棱长为2.
A(2,0,0),E(1,0,2),C(0,2,0),F(1,1,2).
∴
=(-1,0,2),
=(1,-1,2),
∴
·
=-1+0+4=3.
∴cos〈
,
〉
=
,
∴异面直线AE与CF所成角的余弦值为
.
(2)A(2,0,0),B(2,2,0),E(1,0,2),
设
为平面ABE的法向量,则
,
∴
,令
,则可取
,
而
=(1,-1,2),∴
,
所以直线CF与平面ABE所成的角的正弦值为
.
例2.正方体ABEF-DCE′F′中,M、N分别为AC、BF的中点(如图所示),求平面MNA与平面MNB所成锐二面角的平面角的余弦值.
解:
以B为原点,以
的方向为x、y、z轴正方向建立空间直角坐标系B-xyz,设棱长为1,则A(1,0,0),N (
,
,0),M(
,0,
),设面AMN的法向量为
.
则
,令x=1,则可取
.
同理可求出面MNB的法向量可以为
.
.
∴所求二面角的余弦值为
.
例3.在四棱锥
中,侧面
底面
,
,底面ABCD是直角梯形,
,
=90°,
,
.
(1)求证:
平面
;
(2)设Q为侧棱PC上一点,
,
试确定
的值,使得二面角
的平面角为45°.
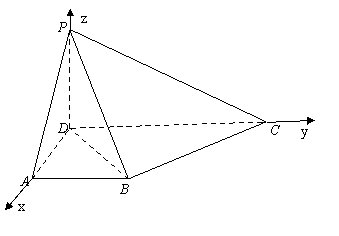
(1)证明:∵面PCD⊥面ABCD,且PD⊥DC,∴PD⊥面ABCD,∴PD⊥AD,而∠ADC=90°,
∴以D为原点,建立如图空间直角坐标系D-xyz,D(0,0,0),B(1,1,0),C(0,2,0).
.
.
∴BC⊥平面PBD.
(2)解:由(1)中,BC⊥平面PBD,∴面PBD的法向量可为
.
设
,记面QBD的法向量为
.
,由
得:
.
令y=1,则可取
.
.
注意到
,解得
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -