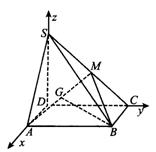
例.在四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,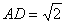 ,DC=SD=2.点M在侧棱SC上,∠ABM=60°.
,DC=SD=2.点M在侧棱SC上,∠ABM=60°.
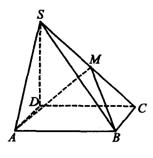
(1)证明:M是侧棱SC的中点;
(2)求二面角S-AM-B的平面角的余弦值.
解:
如图建立空间直角坐标系,设A(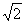 ,0,0),则B(
,0,0),则B(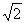 ,2,0),C(0,2,0),S(0,0,2).
,2,0),C(0,2,0),S(0,0,2).
(1)设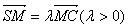 ,
,
则
又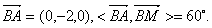 故
故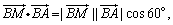
即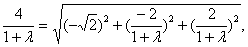 解得λ=1.
解得λ=1.
∴M是侧棱SC的中点.
(2)由M(0,1,1),A(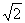 ,0,0)得AM的中点
,0,0)得AM的中点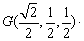
又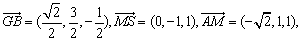
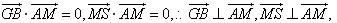
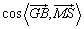 等于二面角S-AM-B的平面角.
等于二面角S-AM-B的平面角.
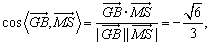
即二面角S-AM-B的平面角的余弦值是-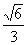 .
.