解析：
解法一：(1)依题设知，AC是所作球面的直径，
则AM⊥MC．又因为PA⊥平面ABCD，则PA⊥CD．
又CD⊥AD，所以CD⊥平面PAD，则CD⊥AM，
所以AM⊥平面PCD，所以平面ABM⊥平面PCD．
(2)由(1)知，AM⊥PD，又PA=AD，则M是PD的中点，
可得AM=2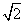
且M到平面ABCD的距离为2，
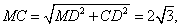
则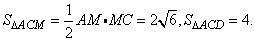
设D到平面ACM的距离为h，由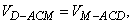
即2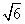
h=8，可求得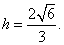
设所求角为θ，则sinθ=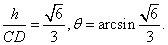
(3)可求得PC=6.因为AN⊥NC，由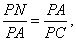
得PN=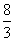
，所以NC∶PC=5∶9.
故N点到平面ACM的距离等于P点到平面ACM距离的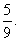
又因为M是PD的中点，则P、D到平面ACM的距离相等，
由（2）可知所求距离为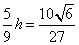
．
解法二：（1）同解法一：
（2）如图所示，建立空间直角坐标系，则A(0，0，0)，P(0，0，4)，B(2，0，0)，C(2，4，0)，D(0，4，0)，M(0，2，2);
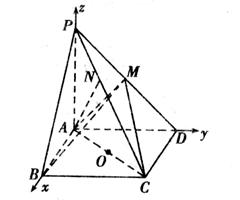
设平面ACM的一个法向量n=(x，y，z)，
由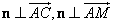
可得
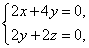令z=1，则n=(2，－1，1).
设所求角为α，则sinα=
，
所求角的大小为arcsin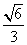
.
(3)由条件可得，AN⊥NC，在Rt△PAC中，
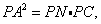所以PN=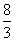
，
则NC=PC－PN=
所求距离等于点P到平面ACM距离的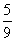
．
设点P到平面ACM的距离为h，
则h=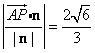
，所以所求距离为
．
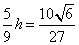