| 简单的逻辑联结词 |
主编:黄冈中学数学集体备课组
思考:下列三个命题间有什么关系?
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除.
1、p且q
一般地,用逻辑联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作
,读作“p且q”.
规定:当p、q都是真命题时,
是真命题;当p、q两个命题中有一个是假命题时,
是假命题.即:全真为真,有假即假.
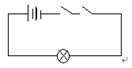
此处原理类似于物理学中串联电路:
开关的闭合与断开对应两个命题的真假,只有在两个开关都闭合时电路才接通.
例1、将下列命题用“且”联结成新命题,并判断它的真假:
(1)p:平行四边形的对角线互相平分;q:平行四边形的对角线相等.
(2)p:菱形的对角线互相垂直;q:菱形的对角线互相平分.
(3)p:35是15的倍数;q:35是7的倍数.
答案:
(1)
:平行四边形的对角线互相平分且相等.因为p真q假,所以
为假命题;
(2)
:菱形的对角线互相垂直且平分.因为p真q真.所以
为真命题;
(3)
:35是15的倍数且是7的倍数.因为p假q真,所以
为假命题.
例2、用逻辑联结词“且”改写下列命题,并判断它们的真假:
(1)1既是奇数,又是素数;
(2)2和3都是素数.
答案:
(1)改写为:1既是奇数且1是素数,因为1是素数为假命题,所以这个命题为假命题;
(2)改写为:2是素数且3是素数,因为“2是素数”与“3是素数”都是真命题,所以这个命题是真命题.
思考:下列三个命题间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数.
2、p或q
一般地,用逻辑联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作:
,读作:p或q.
规定:当p、q两个命题中有一个是真命题时,
是真命题;当p、q都是假命题时,
是假命题.即:全假为假,有真即真.
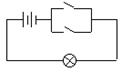
此处原理类似于物理学中并联电路:
开关的闭合与断开对应两个命题的真假,只有在两个开关都断开时电路才断开.
例3、判断下列命题的真假:
(1)2≤2;
(2)集合A是
的子集或是
的子集;
(3)周长相等的两个三角形全等或面积相等的两个三角形全等.
答案:
(1)命题“2≤2”是
、
用“或”联接后构成的命题,因为p是真命题,所以这个命题是真命题;
(2)命题“集合A是
的子集或是
的子集”是由命题:
p:集合A是
的子集、q:集合A是
的子集用“或”联接而成,因为q是真命题,所以这个命题为真命题;
(3)命题:“周长相等的两个三角形全等或面积相等的两个三角形全等”是由两个命题用或联接而成,因为两个命题“周长相等的两个三角形全等”与“面积相等的两个三角形全等”都为假命题,所以这个命题为假命题.
思考:如果
为真命题,那么
一定是真命题吗?反之,如果
为真命题,那么
一定是真命题吗?
答案:
如果
为真命题,则p、q都是真命题,从而
一定是真命题;反之,如果
为真命题,只能得到p、q中至少有一个是真命题,从而
不一定是真命题.
注意:
逻辑联结词中的“或”相当于集合中的“并集”,它与日常用语中的“或”的含义不同.日常用语中的“或”是两个中任选一个,不能都选,而逻辑联结词中的“或”,可以是两个都选,但又不只(备注:视频中漏掉了“只”字)是两个都选,而是两个中至少选一个,因此,有三种可能的情况.
逻辑联结词中的“且”相当于集合中的“交集”即两个必须都选.
思考:下列命题间有什么关系?
(1)35能被5整除;
(2)35不能被5整除.
3、非p
一般地,对一个命题p全盘否定,就得到一个新命题,记作:
p,读作“非p”或“p的否定”.
若p是真命题,则
必是假命题;若p是假命题,则
必是真命题.
“非”命题最常见的几个正面词语的否定:
正面 |
|
|
是 |
都是 |
至多有一个 |
至少有一个 |
任意的 |
所有的 |
否定 |
|
≤ |
不是 |
不都是 |
至少有两个 |
一个也没有 |
某个 |
某些 |
例4、写出下列命题的否定,并判断它们的真假:
(1)p:
是周期函数;
(2)p:3<2;
(3)p:空集是集合A的子集;
(4)p:
是无理数;
(5)p:x=2且y=3.
答案:
(1)
p:
不是周期函数.命题p为真命题,
p是假命题;
(2)
p:
.命题p为假命题,
p是真命题;
(3)
p:空集不是集合A的子集.命题p为真命题,
p是假命题;
(4)
p:
不是无理数.命题p为真命题,
p是假命题;
(5)
p:
例5、分别指出下列命题的形式及构成它的简单命题.
(1)24既是8的倍数,又是6的倍数;
(2)李强是篮球运动员或跳水运动员;
(3)平行线不相交.
答案:
(1)该命题是
形式,简单命题是p:24既是8的倍数,q:24是6的倍数;
(2)该命题是
形式,简单命题是p:李强是篮球运动员,q:李强是跳水运动员;
(3)该命题是
形式,简单命题是p:平行线相交.
例6、已知a>0,a≠1,设p:函数y=loga(x+1)在(0,+∞)上单调递减;q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p且q为假命题,p或q为真命题,求a的取值范围.
解:
若p为真,则0<a<1.若q为真,则x2+(2a-3)x+1=0有两个不同实数解.
∴Δ=(2a-3)2-4>0解得a<
或a>
.
∵p且q为假,p或q为真,∴p与q中有且只有一个为真命题.
(1)当p真q假时,则
.
(2)当p假q真时,则
,又
,∴
.
综上所述,a的取值范围为[
,1)∪(
,+∞).
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -